2 Graphiques et visualisation de données
"If anything, there should be a Law: Thou Shalt Not Even Think Of Producing A Graph That Looks Like Anything From A Spreadsheet. — T. Harding
2.1 Vue d’ensemble
R propose plusieurs systèmes de graphiques, présentant des caractéristiques bien différentes. Les plus communs sont :
- R base : C’est le système d’origine. Il faut le considérer comme une page blanche, sur laquelle on rajoute tous les éléments du graphique manuellement, un par un en ajoutant de nouvelles lignes de code. Il apporte une flexibilité maximale, mais au prix d’un code complexe, et difficile à appréhender en termes de structures des données.
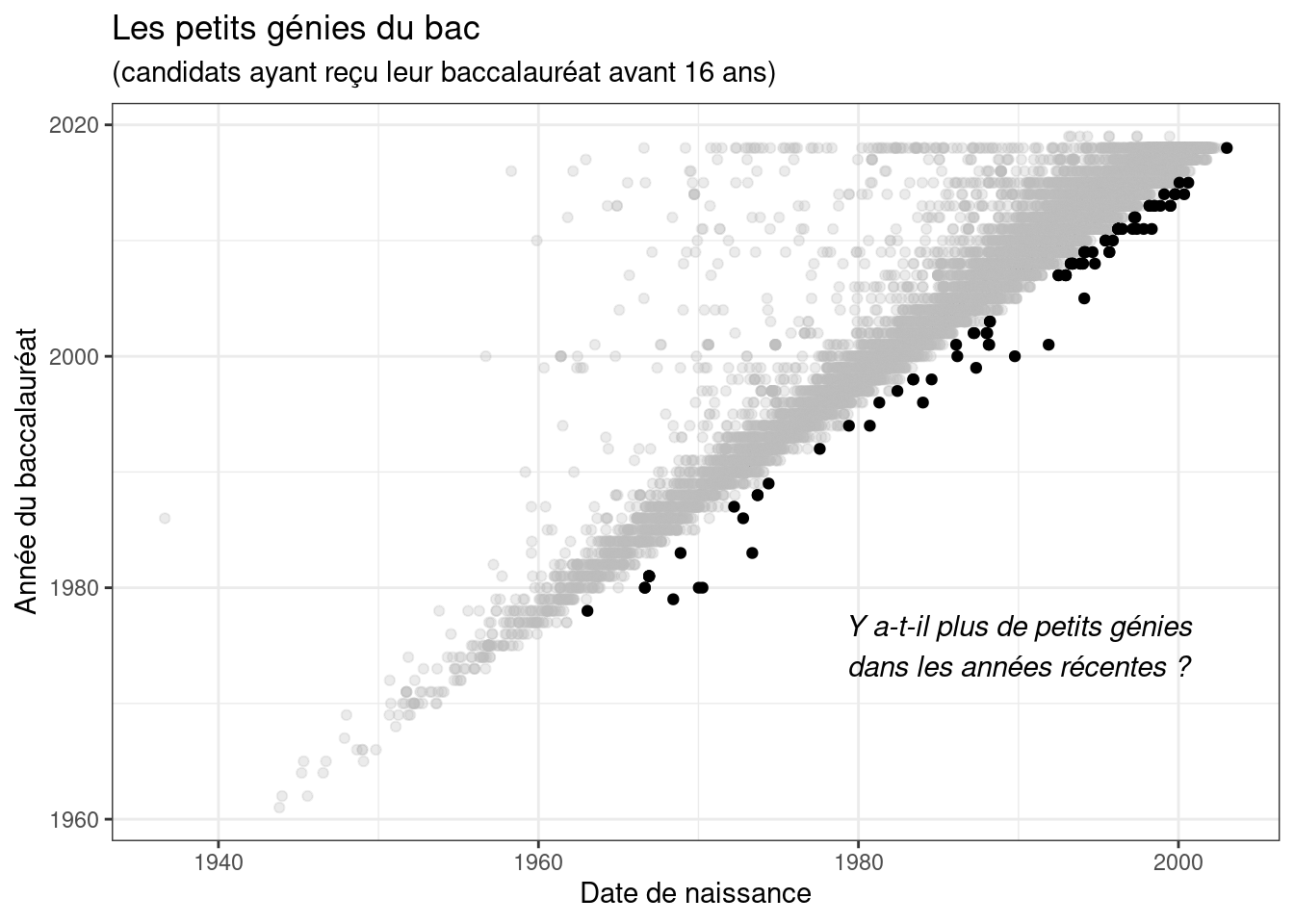
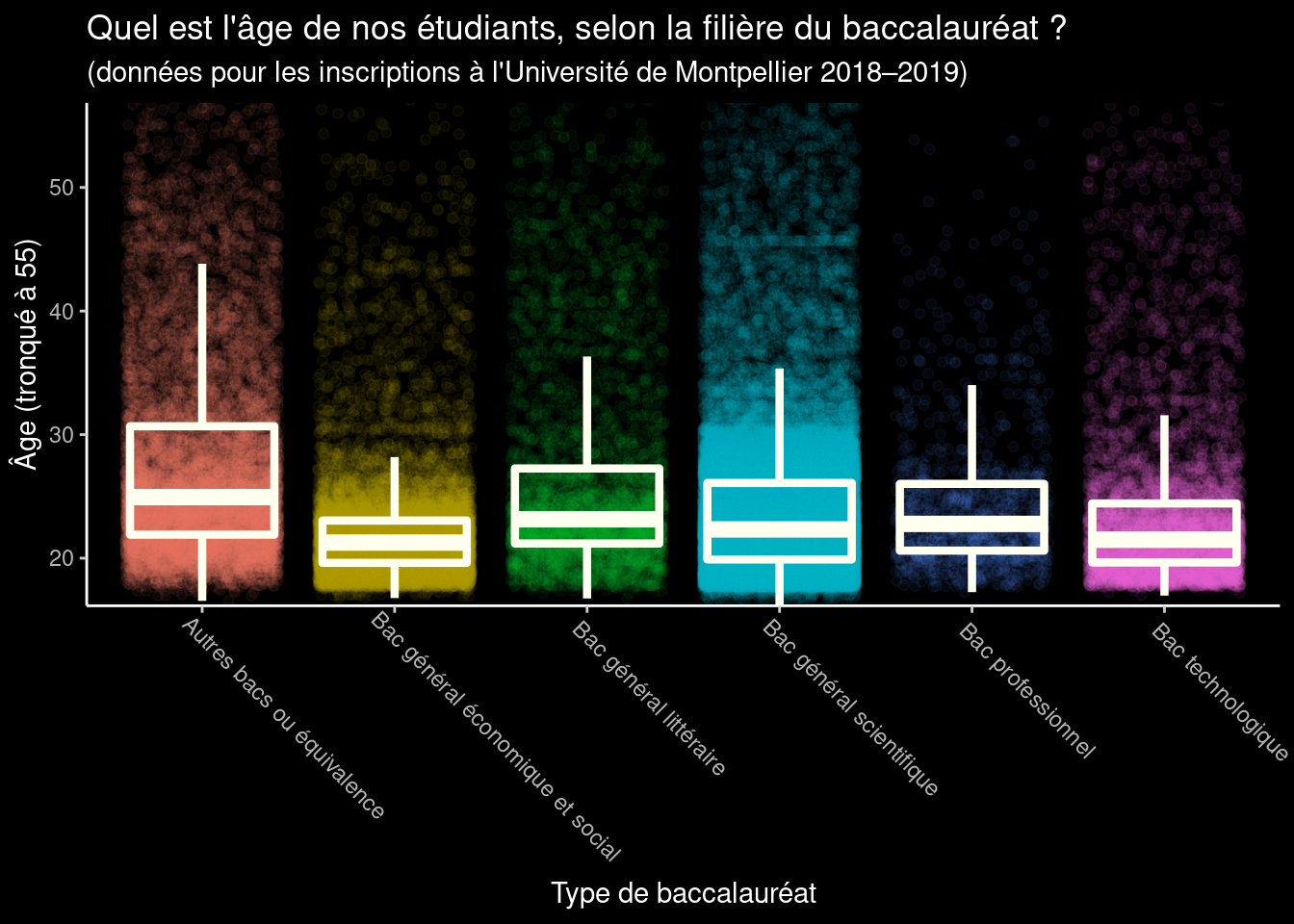
lattice: Il s’agit d’une première approche d’automatisation des graphiques au sein d’une fonction unique, qui prend en charge la plupart des paramètres, et gère un certain nombre de tâches automatiquement. Il devient en revanche beaucoup plus compliqué d’arriver exactement à ce qu’on souhaite, maislatticepeut être très utile pour des graphiques conditionnels.ggplot2: C’est le système de graphiques pour des sorties de qualité de publication. Il utilise la même idée quelattice(une fonction s’occupe de tout), mais en s’appuyant sur une grammaire des graphiques orientée données très puissante et relativement intuitive. C’est ce système que nous allons explorer ici. Il permet par exemple de faire ce genre de choses sans que cela soit trop compliqué :
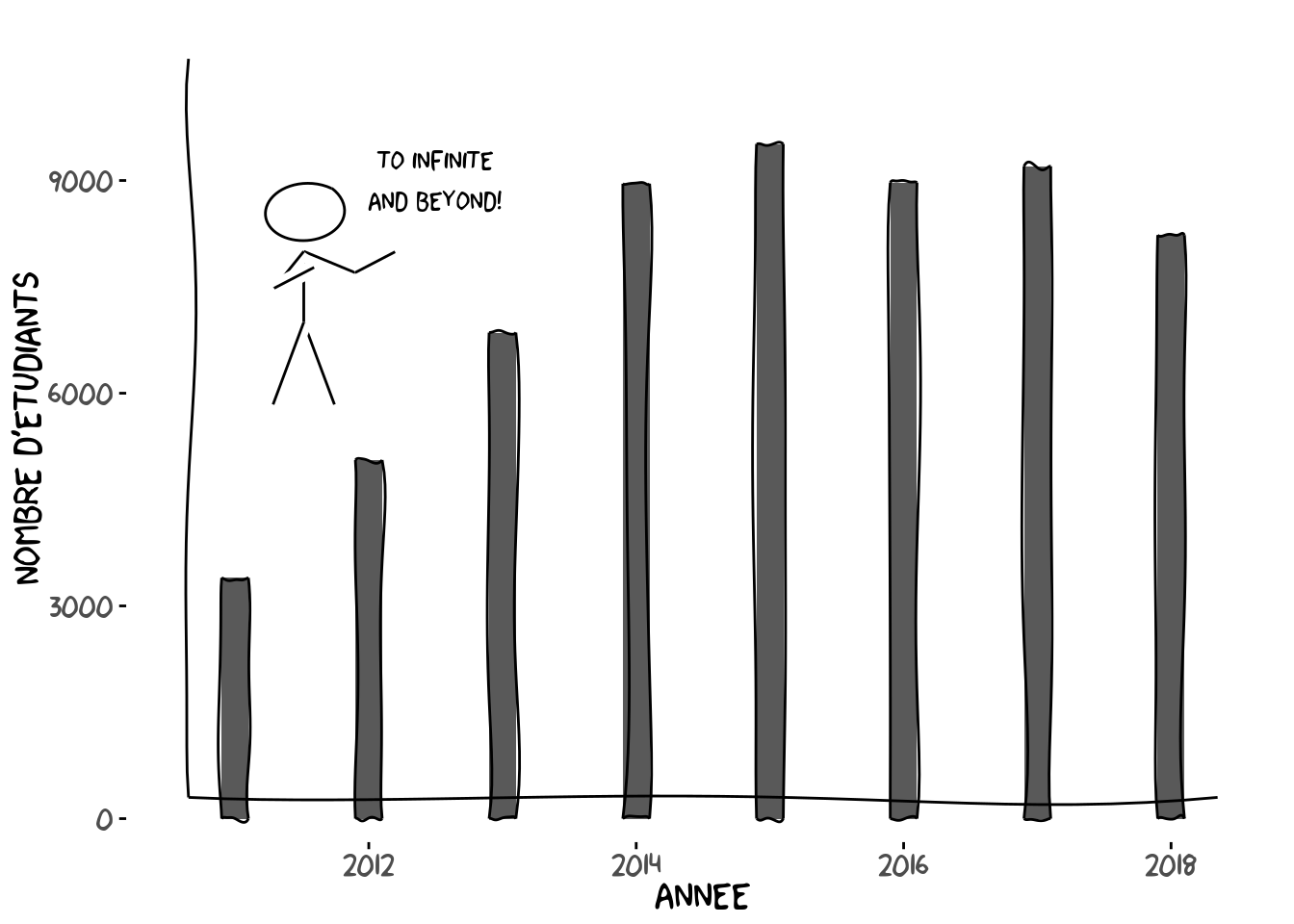
2.2 Le package ggplot2
2.2.1 La grammaire des graphiques
ggplot2 est un package dont le développement remonte à plus de 15 ans, une
éternité à l’échelle de R ! Ce package a un objectif unique, faire des
graphiques de qualité supérieure, s’appuyant sur la grammaire des graphiques,
un paradigme de visualisation orienté données. On peut résumer ggplot2 par une
question simple : « Comment visualiser ce tableau de données ? »
La grammaire des graphiques s’appuye sur quatre éléments essentiels d’un graph :
- Les données et leur cartographie :
ggplot2attend un tableau de données (data.frame) dans lequel chaque ligne est un individu (au sens statistique) et chaque colonne une variable. Nous reviendrons plus tard sur cette organisation fondamentale des données en individus-variables. La cartographie (mapping) des données consiste simplement à indiquer quelles variables utiliser pour quels axes — noter bien qu’il y a possiblement plus de deux axes dans un graphique, même 2D : on peut y rajouter un axe de couleurs ou un axe de formes. - Les géométries : Une fois qu’on a défini les axes du graphique, il faut donc décider de la représentation de ces données. Est-ce que l’on souhaite un nuage de points, des lignes, une boîte à moustaches, un histogramme, ou bien d’autres formes plus complexes ?
- Les échelles : Il s’agit ici de préciser le systèmes de coordonnées. Par défaut, on travaille en espace carthésien, mais il est parfois utile d’avoir un axe en échelle logarithmique, ou bien de préciser l’échelle des couleurs de manière plus efficace pour la visualisation. Les échelles se rapportent aux axes du graphique — rappelons-nous qu’il y a en a souvent plus de deux !
- La décoration : Finalement, au-delà de l’information présentée par le graphique, on peut ajuster (et améliorer) tous les éléments de style, et s’appuyer sur tout un ensemble de thèmes pré-définis.
2.2.2 Extensions et ressources indispensables
Il existe tout un écosystème d’extensions
qui ajoutent aux possibilités de ggplot2 (nouveaux types de graphiques,
fonctionnalités supplémentaires, thèmes, etc.). Parmi les plus notables, on peut
lister les suivantes (qui ne seront pas utilisées dans cette formation) :
gganimate, qui permet d’animer des graphiques avec des transitions totalement fluide entre graphiques ;gghighlight, qui met en évidence des valeurs spécifiques dans les graphiques (points, lignes, histogrammes, etc.) ;ggrepel, qui fournit des annotations et étiquettes qui ne se chevauchent pas ;patchwork, qui permet d’arranger plusieurs graphiquesggplot2sur une seule figure ;viridis, qui introduit des palettes de couleurs compatibles avec les anomalies de la vision de type daltonisme.
Un certain nombre de ressources absolument indispensables concernant ggplot2
et la dataviz sont également disponibles sur le web :
- R Graph Gallery (en anglais) : une galerie de plus de 400 graphiques, triés par type de graph, avec le code pour les reproduire, ainsi qu’une description incluant les chausse-trapes pour chaque graphique.
- From Data to Viz (en anglais) : en complément du précédent, une manière interactive de préparer ses graphiques selon la structure des données et le résultat souhaité, en suivant un arbre de décision.
- Fundamentals of Data Visualization (en
anglais) : un bouquin fantastique sur la dataviz, qui décrit tous les concepts
sous-jacents à un bon graphique, de l’utilisation de l’espace blanc aux
couleurs, pour tous les types de données possibles. Entièrement préparé sous R,
le code source (qui utilise
ggplot2) est intégralement disponible.
2.3 Données et géométries
2.3.1 Mon premier graphique ggplot2 : Histogrammes
Le minimum pour un graphique ggplot2 est de spécifier les données et leur
cartographie, et le type de géométrie à utiliser, selon la syntaxe :
ggplot(data = <DATA>, mapping = aes(<MAPPINGS>)) +
<GEOM_FUNCTION>()On rajoute ensuite les éléments supplémentaires (autres géométries, échelles,
décorations) comme des couches supplémentaires avec l’opérateur +.
En pratique, on va utiliser les données d’inscription à l’Université de Montpellier (année 2018–2019) que l’on chargera directement avec la commande suivante :
load("data/um18.RData")
um18[1:5, 1:7]# A tibble: 5 x 7
decede annee_univ idetu civilite date_naiss code departement_pays
<chr> <dbl> <dbl> <chr> <dttm> <chr> <chr>
1 non 2018 1035789 Mme 2000-10-05 00:00:00 84 VAUCLUSE
2 non 2018 2211839 M 1997-06-16 00:00:00 6 ALPES MARITIMES
3 non 2018 2211840 M 2000-04-13 00:00:00 84 VAUCLUSE
4 non 2018 921768 Mme 1993-10-08 00:00:00 205 LIBAN
5 non 2018 921685 Mme 1994-10-02 00:00:00 352 ALGERIE On commence donc par charger le package :
library("ggplot2")Puis on utilise la syntaxe de ggplot2 pour visualiser la distribution
(univariée) selon un histogramme de fréquence (géométrie geom_histogram()) :
ggplot(um18, aes(x = prem_insc_univ_fr)) +
geom_histogram()`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.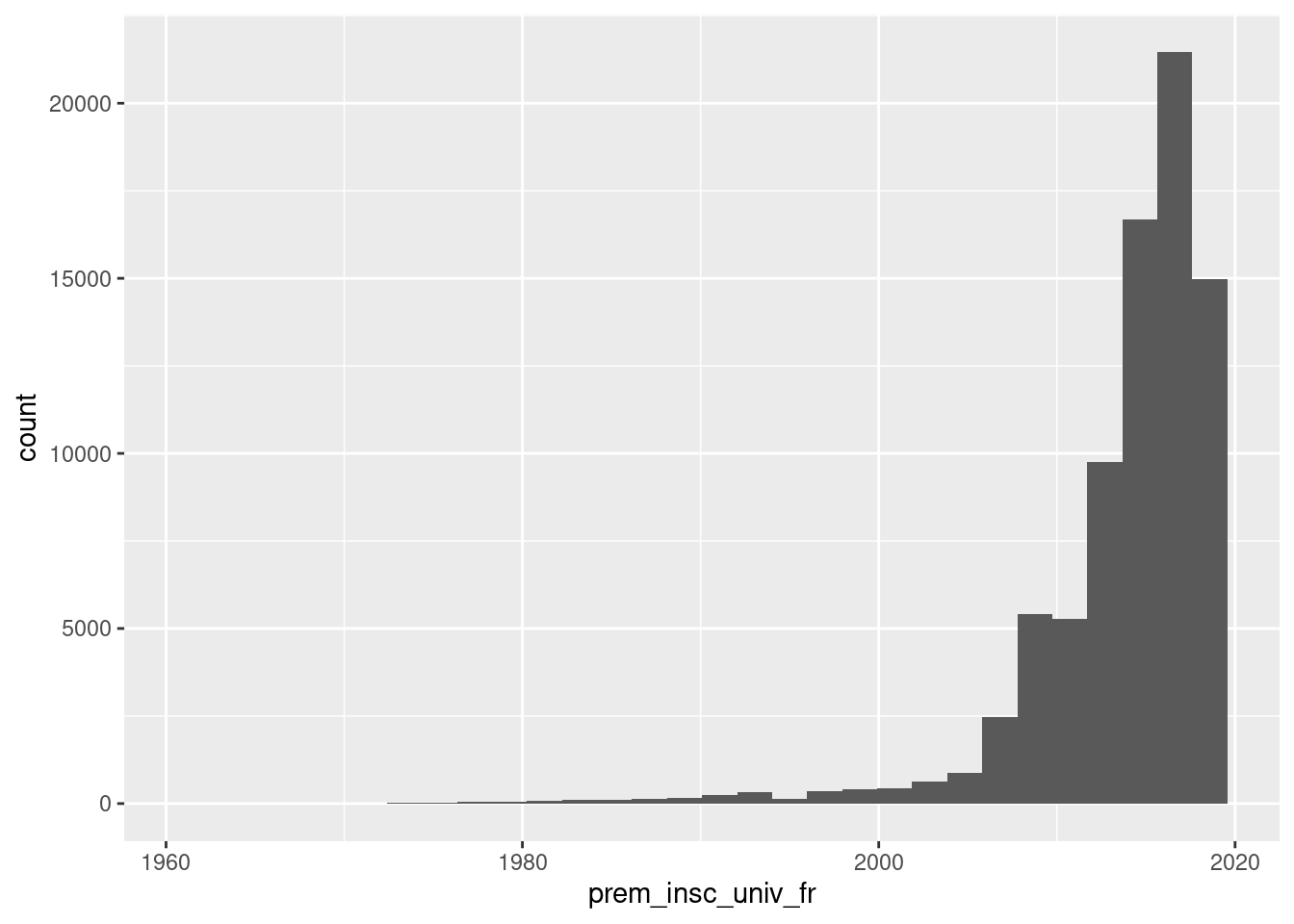
Ce n’est pas si mal, tous les éléments y sont ! Il y a bien sûr plusieurs choses
à ajuster sur la décoration, mais il semble surtout y a voir bizarrement une
diminution sur la dernière année… Regardons cela de plus près en fixant la
largeur des classes de l’histogramme en utilisant le paramètre binwidth de la
fonction geom_histogram() comme indiqué :
table(um18$prem_insc_univ_fr)
1962 1964 1965 1966 1967 1969 1970 1971 1972 1973 1974 1975 1976
1 1 1 4 1 2 8 4 4 10 9 14 13
1977 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989
15 27 23 16 33 40 53 61 37 75 59 63 79
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002
84 95 148 193 121 147 167 189 201 202 177 253 278
2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015
355 410 475 925 1540 2262 3153 2707 2571 4002 5762 8148 8521
2016 2017 2018 2019
9317 12156 14972 4 ggplot(um18, aes(x = prem_insc_univ_fr)) +
geom_histogram(binwidth = 1)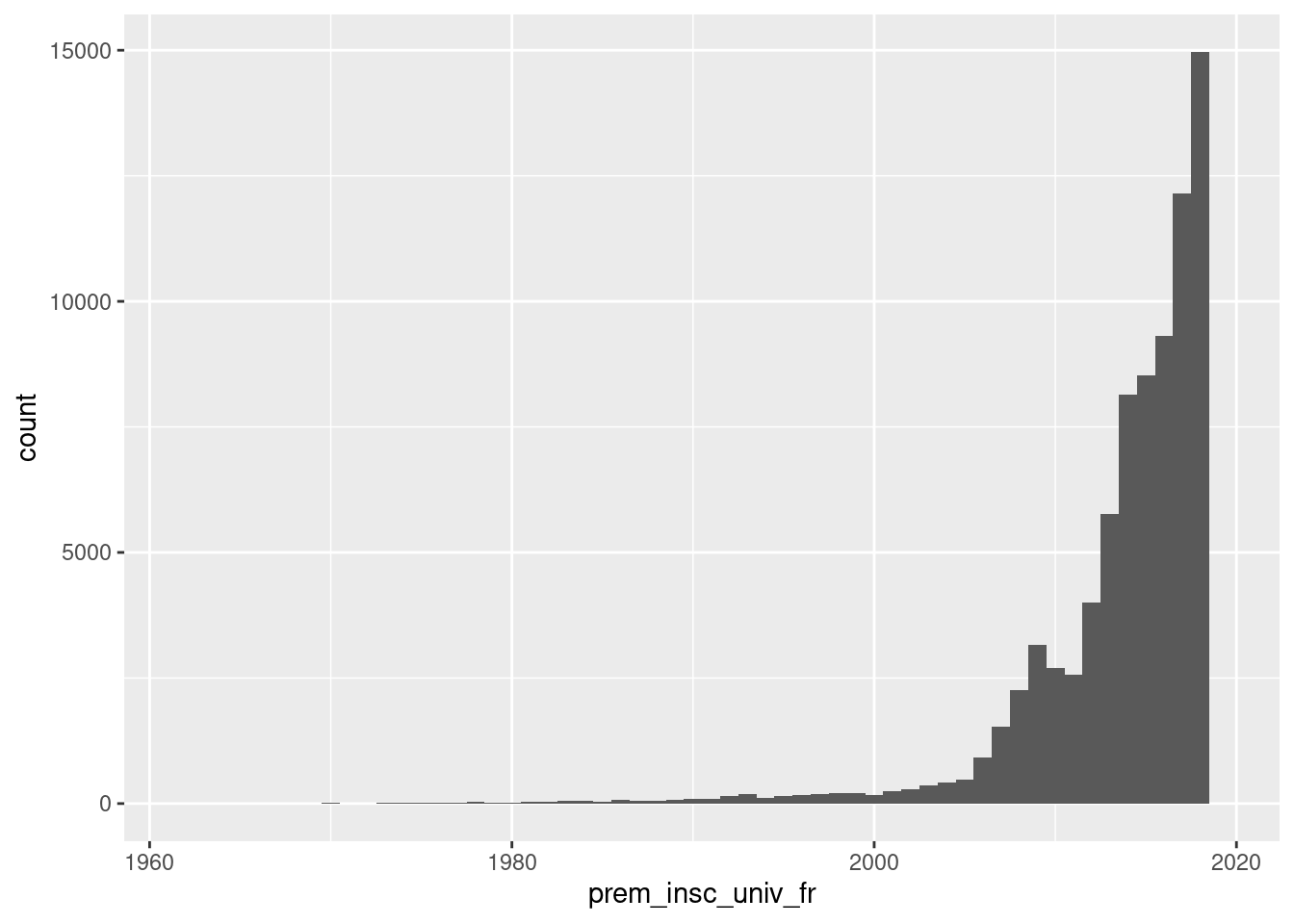
Cette fois, la distribution est bien visible, avec un pic en 2018 comme attendu.
On aurait tout aussi bien pu spécifier les limites de classes manuellement via
le paramètre breaks :
ggplot(um18, aes(x = prem_insc_univ_fr)) +
geom_histogram(breaks = seq(from = 1960, to = 2020, by = 5))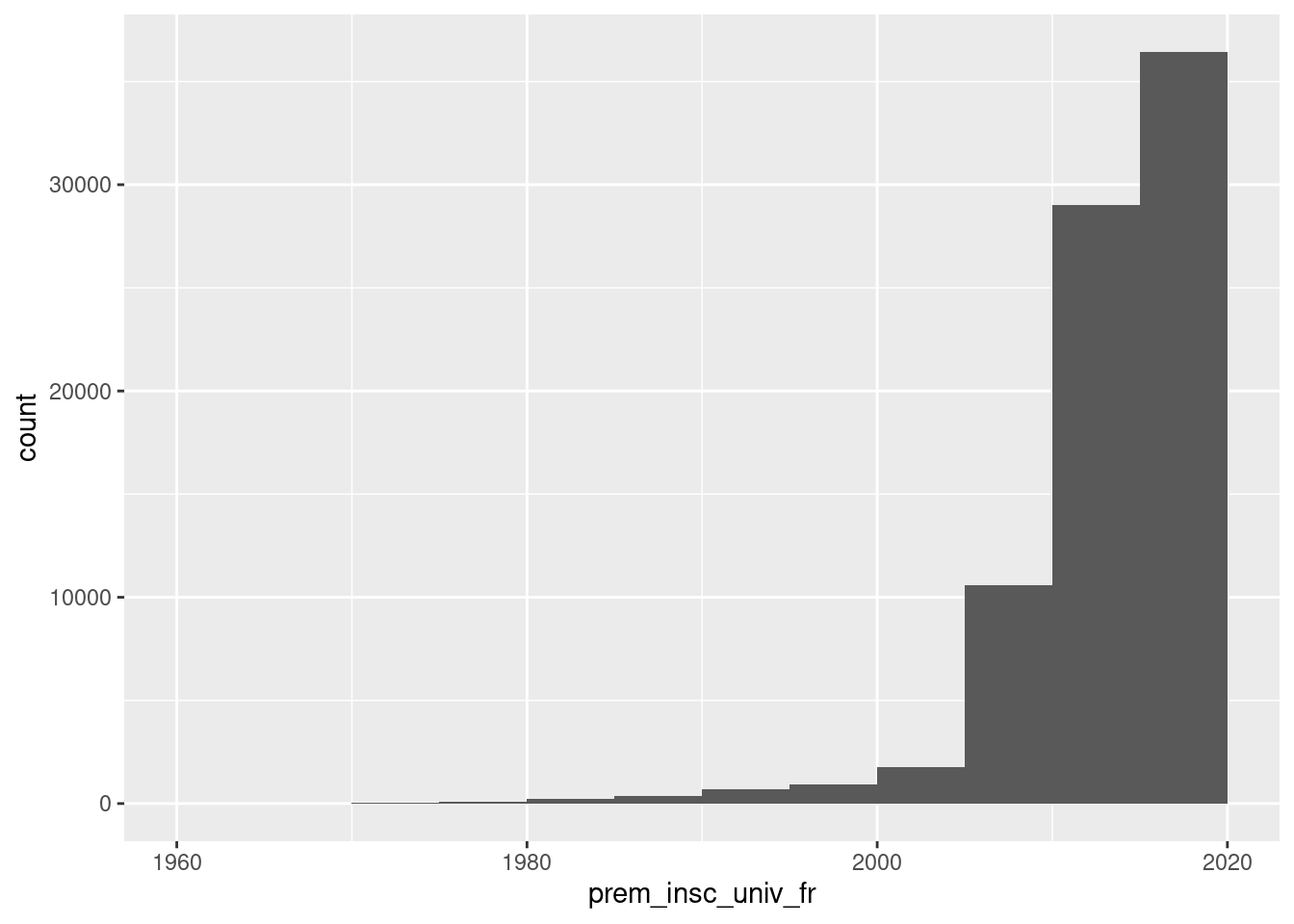
2.3.2 Boîtes à moustaches
Si l’on n’est pas forcément intéressé par la forme précise de la distribution,
on peut utiliser un des outils de base des statistiques : les boîtes à
moustaches (geom_boxplot()). Pour avoir ce diagramme verticalement, on définit
cette fois la variable Prem_insc_univ_fr comme l’axe des Y :
ggplot(um18, aes(y = prem_insc_univ_fr)) +
geom_boxplot()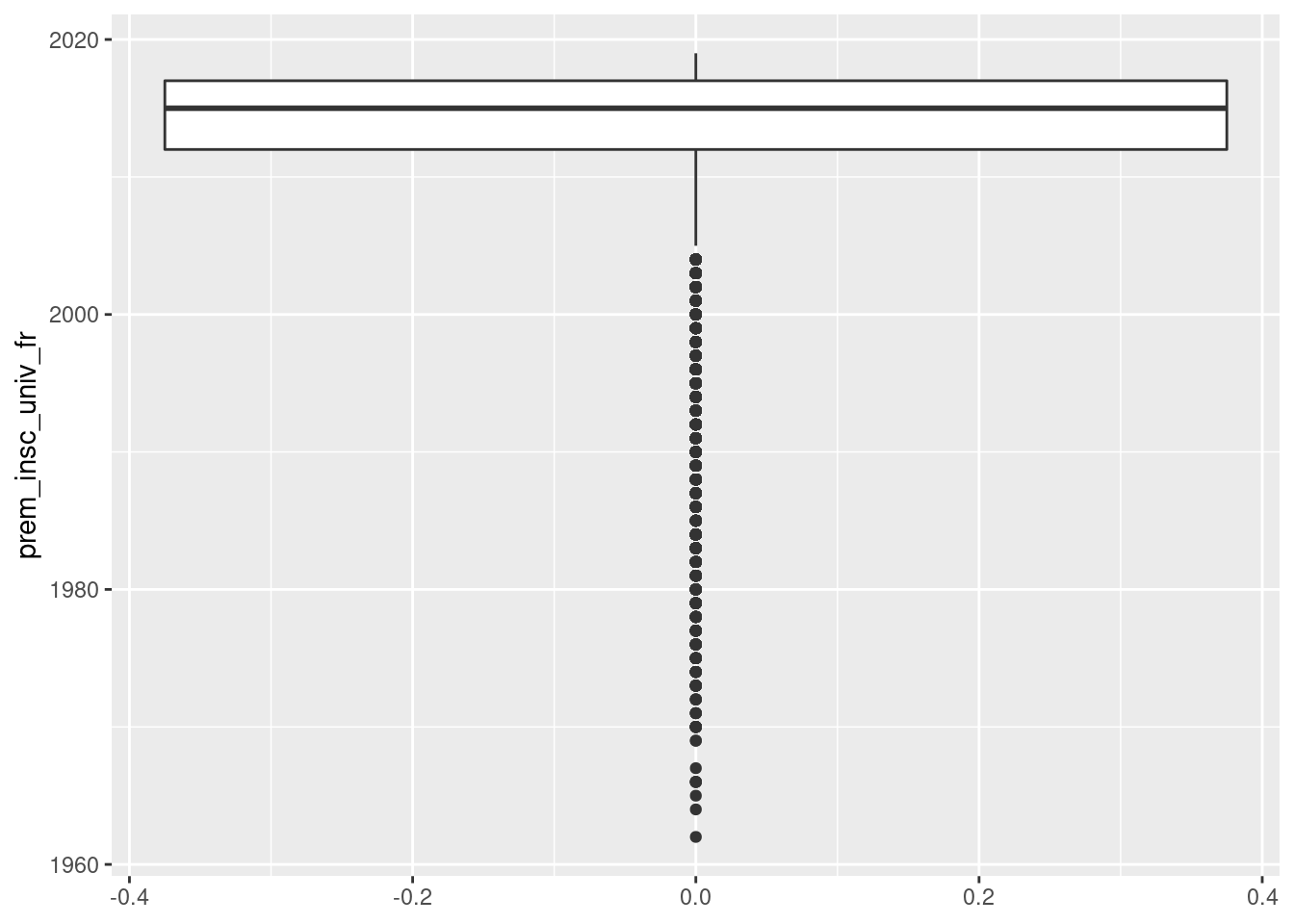
Ce graphique n’apporte pas grand chose d’intéressant en soi, mais les boîtes à
moustaches deviennent très intéressantes quand on les croise avec une variable
qualitative à plusieurs modalités, par exemple le type de baccalauréat. Par
commodité, on a créé une variable $bac_abr qui reprend la variable
$bac_regroup de manière abrégée :
ggplot(um18, aes(x = bac_abr, y = prem_insc_univ_fr)) +
geom_boxplot()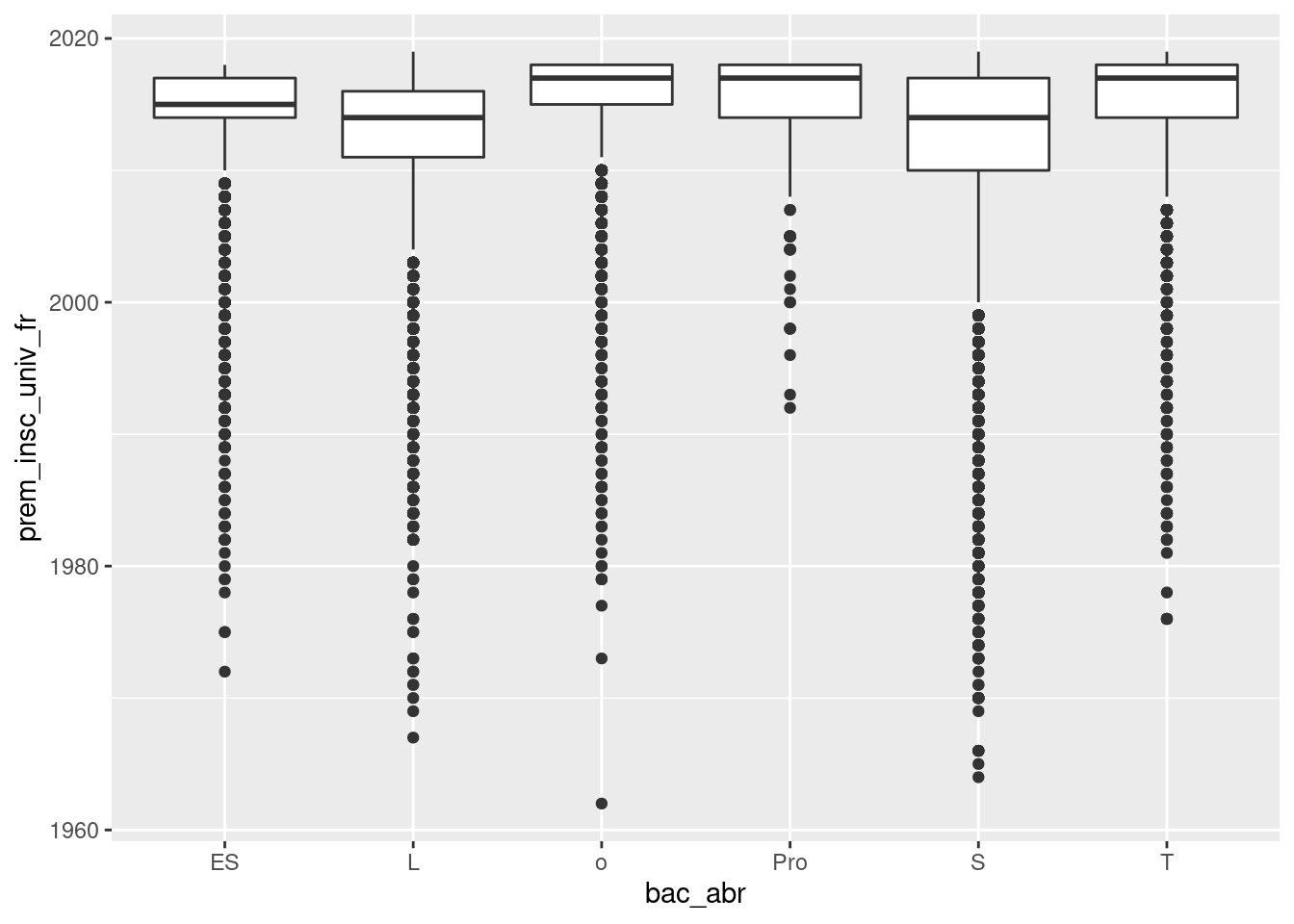
2.3.3 Nuages de points
Le nuage de points est l’outil de base pour visualiser deux variables continues.
Ce type de graphique sera couvert rapidement ici à l’aide de la géométrie
geom_point :
ggplot(um18, aes(x = prem_insc_univ_fr, y = date_naiss)) +
geom_point()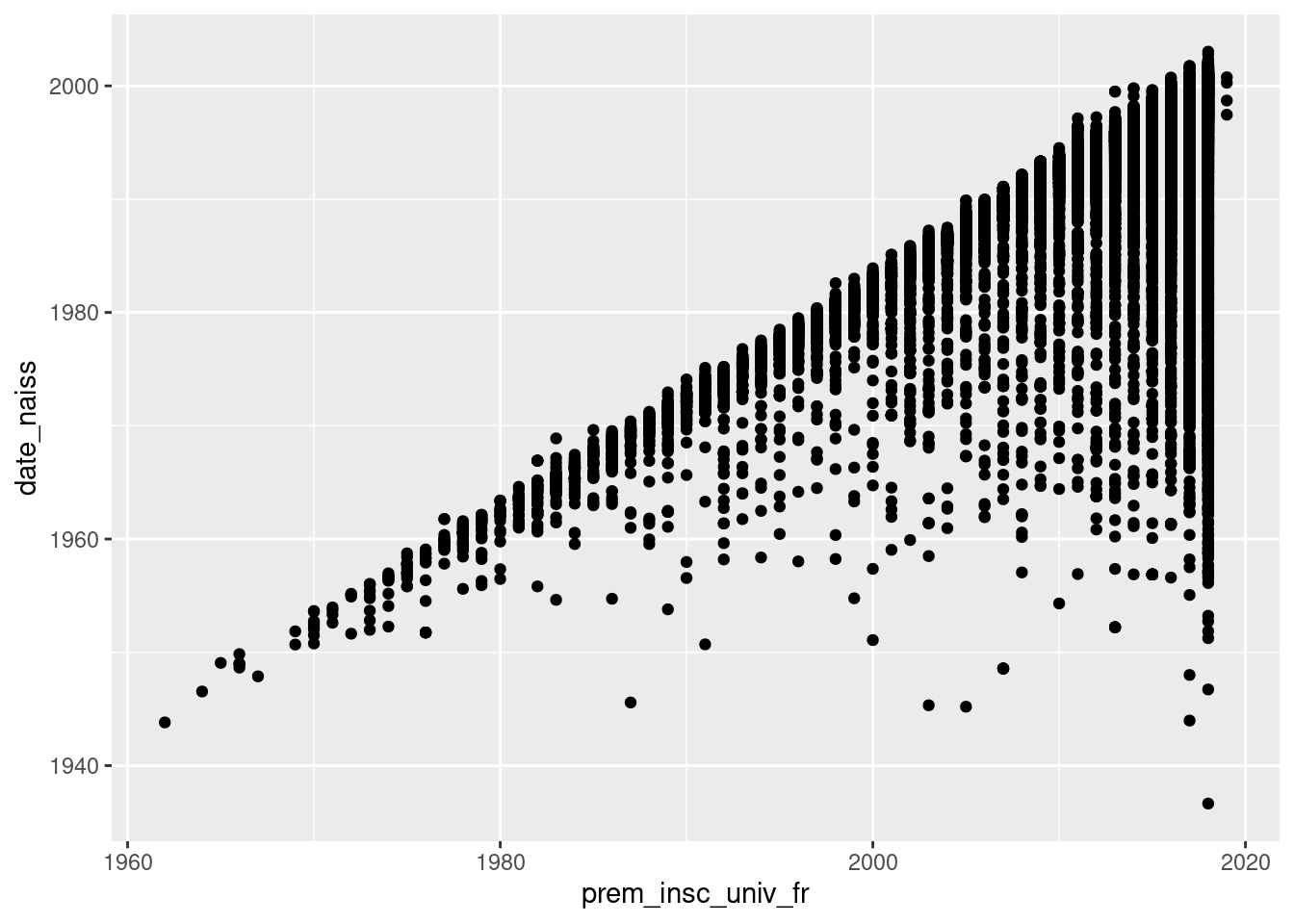
Il sera toutefois l’occasion de présenter la gestion de la transparence par le
package ggplot2, via le paramètre alpha :
ggplot(um18, aes(x = prem_insc_univ_fr, y = date_naiss)) +
geom_point(alpha = 0.1)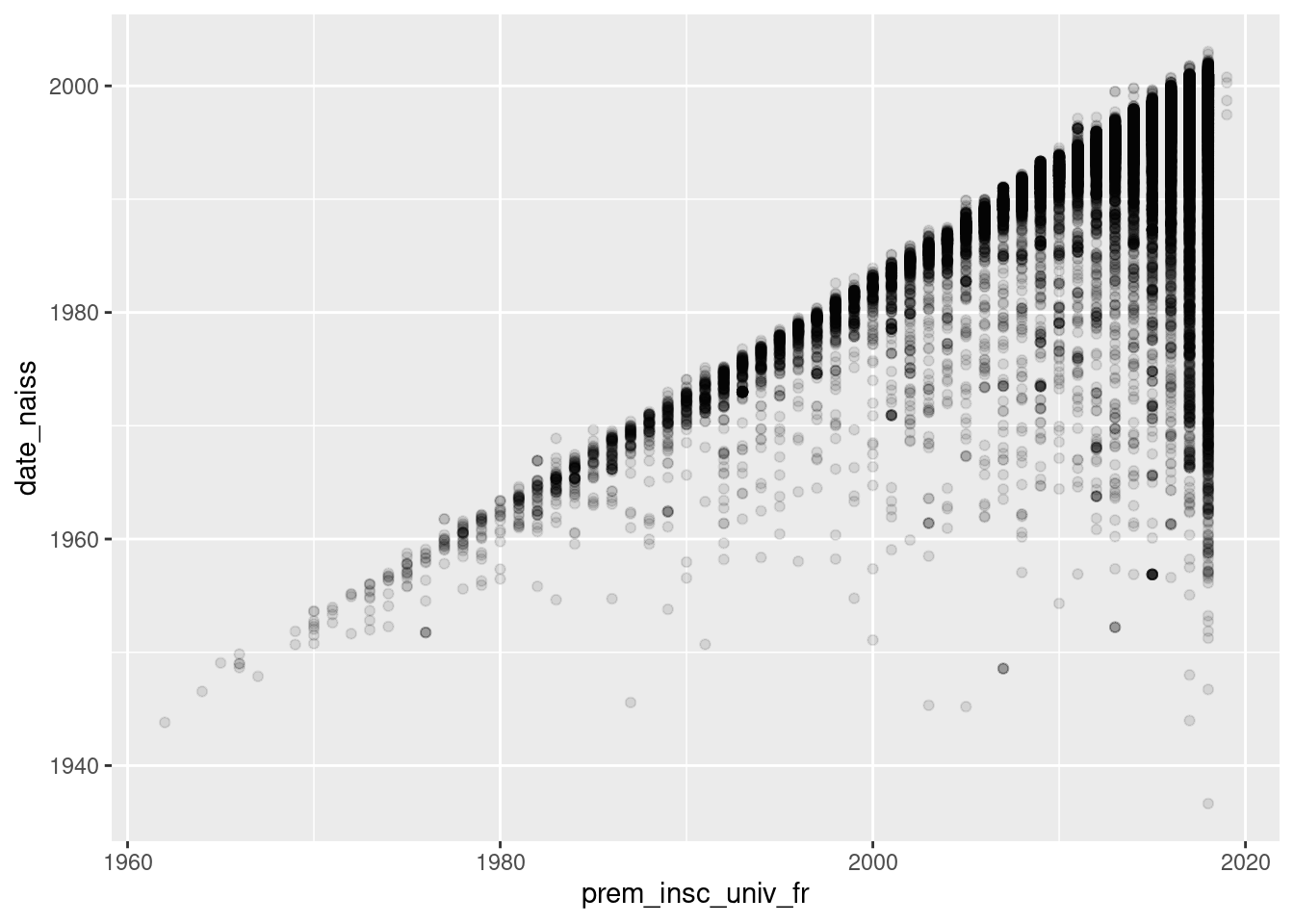
Il semble que l’on ait de plus en plus d’étuidants âgés inscrits à l’université.
On peut ajuster automatiquement un modèle aux données via geom_smooth(). On
utilisera geom_smooth(method = lm) si l’on attend une relation linéaire entre
les deux variables ; par défaut, geom_smooth() lisse les données via un modèle
additif généralisé (GAM) :
ggplot(um18, aes(x = prem_insc_univ_fr, y = date_naiss)) +
geom_point(alpha = 0.1) +
geom_smooth()`geom_smooth()` using method = 'gam' and formula 'y ~ s(x, bs = "cs")'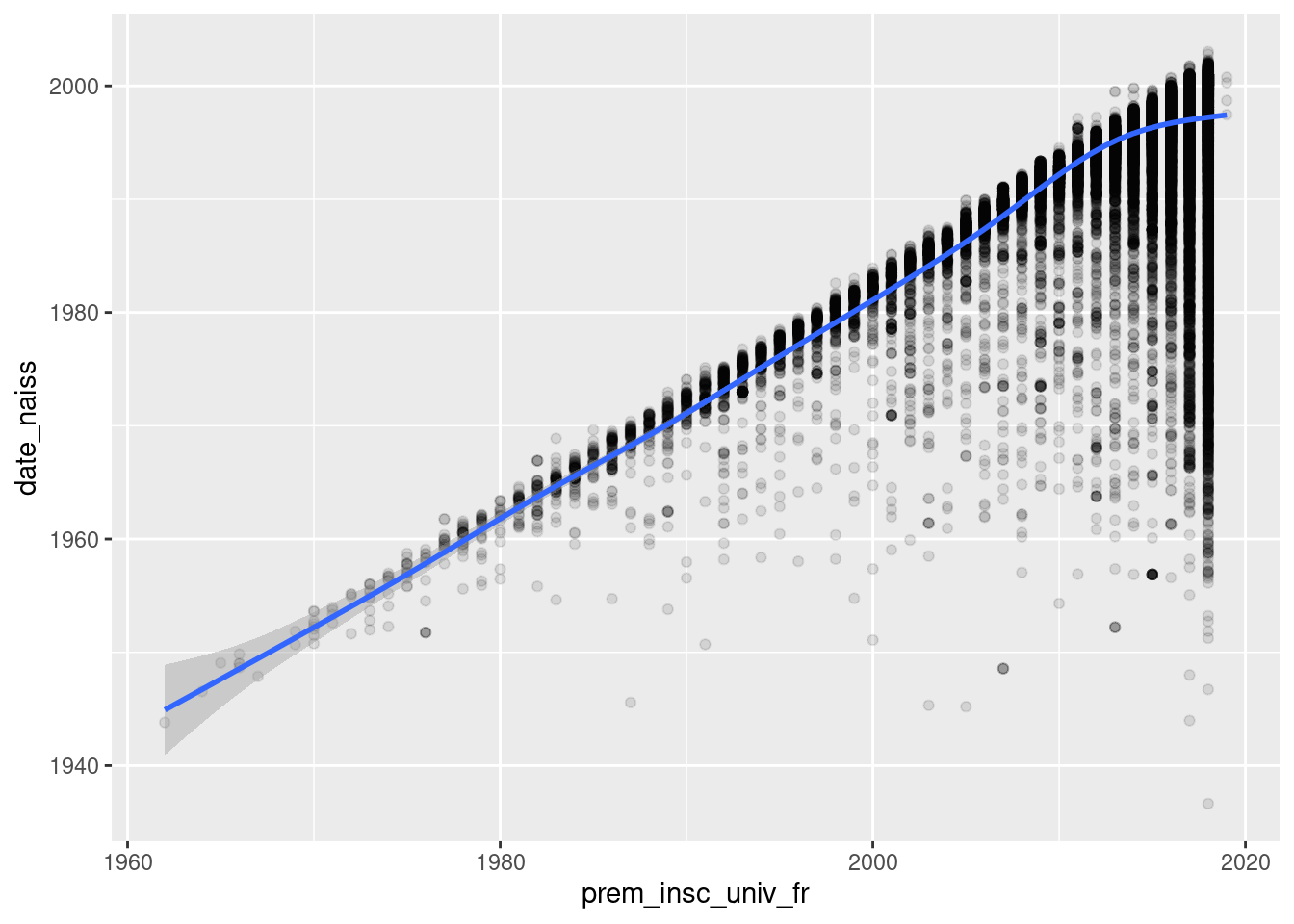
À noter : Parmi les géométries les plus courantes non-traitées dans cette formation, il existe également geom_line(), qui est très utile pour visualiser des séries temporelles, pour lesquelles on a des valeurs répétées par individu (au sens statistique) au cours du temps.
2.4 Les échelles
2.4.1 Diagrammes en barres
Puisque l’on s’intéresse aux types de bac, on va visualiser simplement le nombre
d’inscrits selon chaque type, en utilisant un diagramme en barres (geom_bar())
:
table(um18$bac_abr)
ES L o Pro S T
13667 4051 9775 1089 45537 6069 ggplot(um18, aes(x = bac_abr)) +
geom_bar()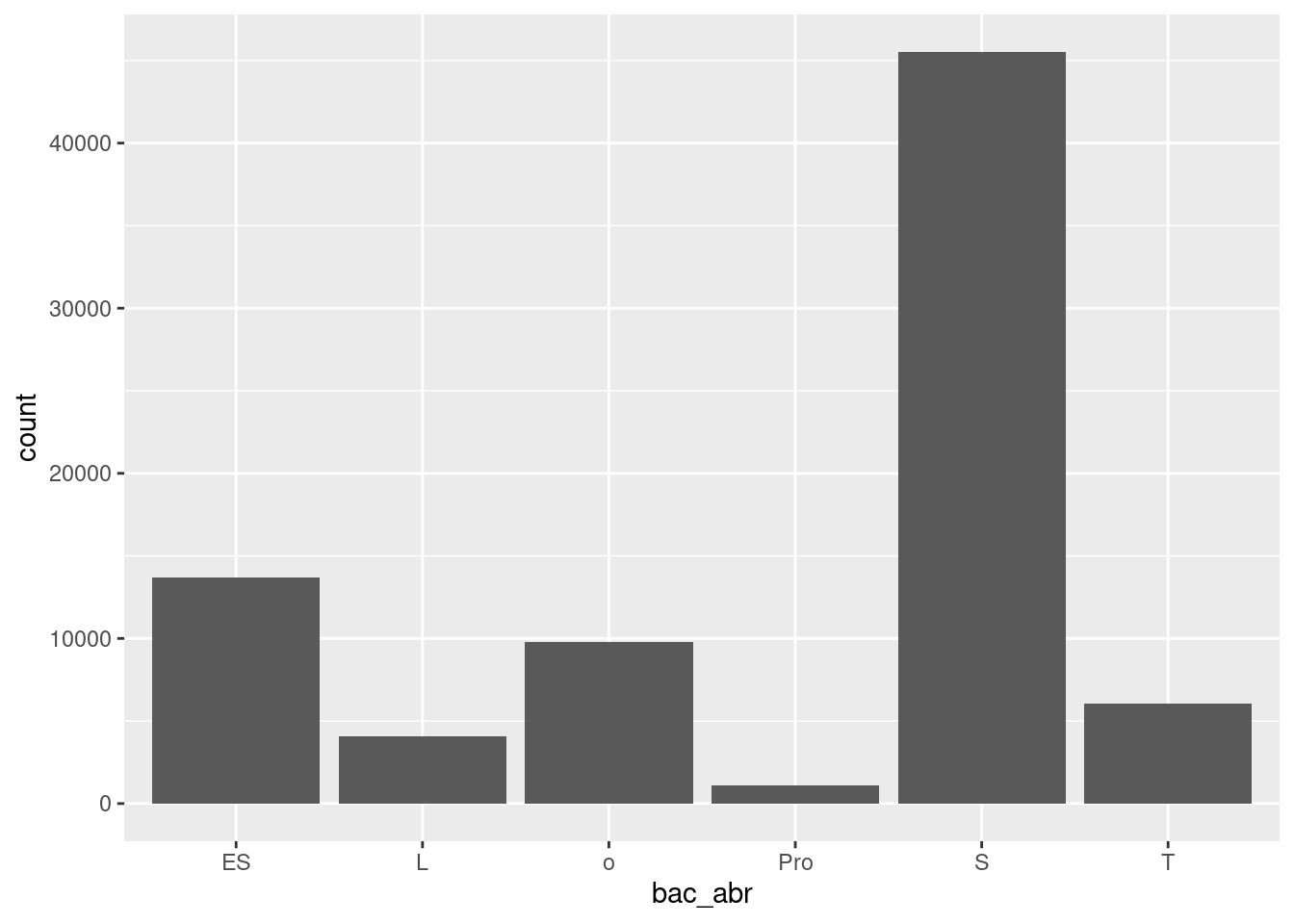
On pourrait vouloir empiler ces barres… ce qui est compliqué ici, vu que cela
nous supprimerait notre seul axe d’information, l’axe des X ! On va ruser un peu
en utilisant comme axe des X une variable qui comporte une modalité unique pour
tous les étudiants : l’année d’inscription en cours (2018 pour tout le monde).
On peut alors utiliser le type de bac comme variable de regroupement via la
couleur de remplissage (paramètre fill) :
ggplot(um18, aes(x = annee_univ, fill = bac_abr)) +
geom_bar()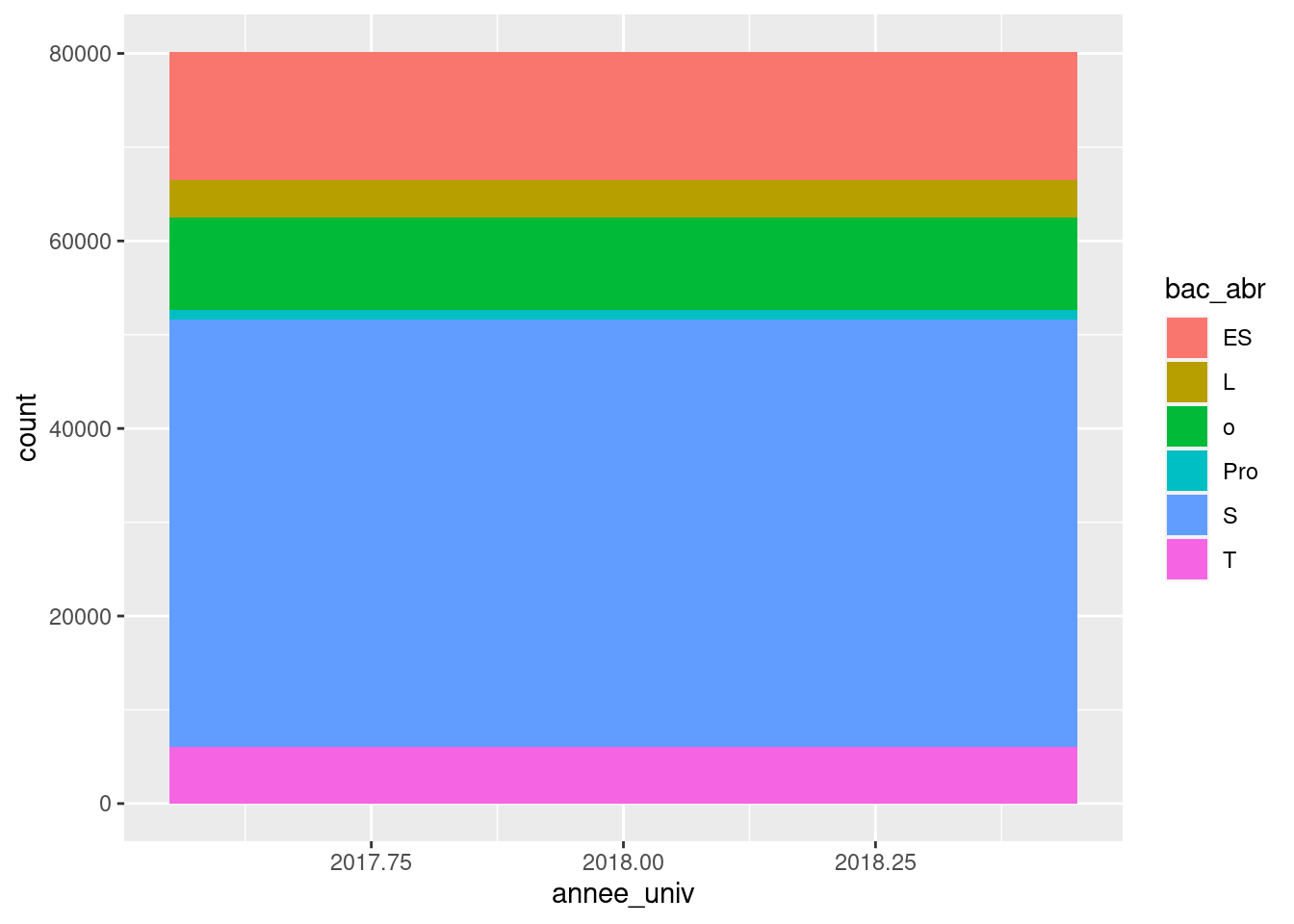
On y est presque, mais l’axe des X considère l’année comme une variable continue, ce qui n’est pas du meilleur effet. On peut tricher en peu en déclarant la variable comme une chaîne de caractères. On en profite également pour réduire la largeur de la colonne :
ggplot(um18, aes(x = as.character(annee_univ), fill = bac_abr)) +
geom_bar(width = .5)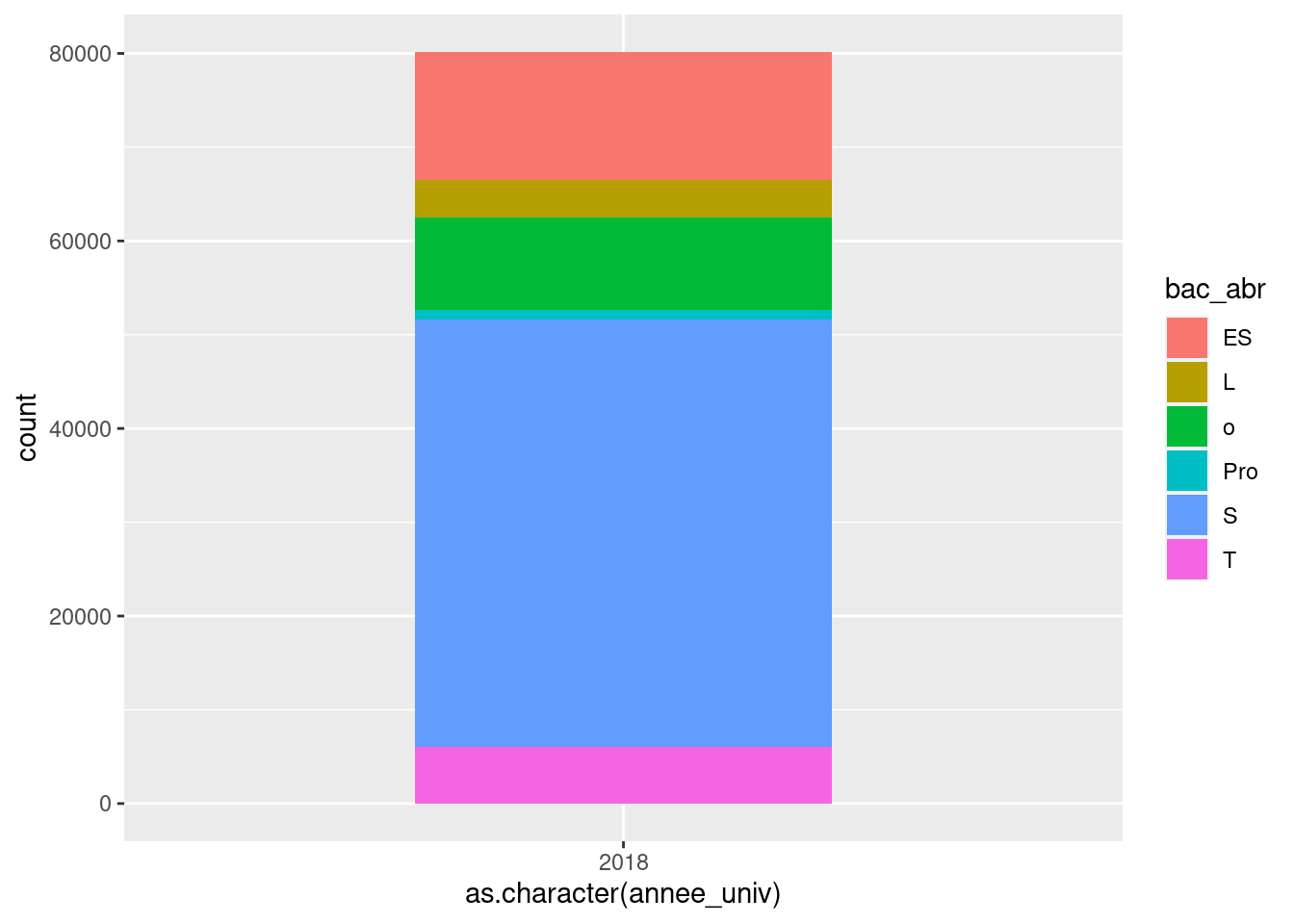
La fonction coord_flip() agit directement sur les axes pour intervertir l’axe
des X et l’axe des Y. Cela nous permet d’avoir un bandeau horizontal selon le
type de bac :
ggplot(um18, aes(x = as.character(annee_univ), fill = bac_abr)) +
geom_bar(width = .25) +
coord_flip()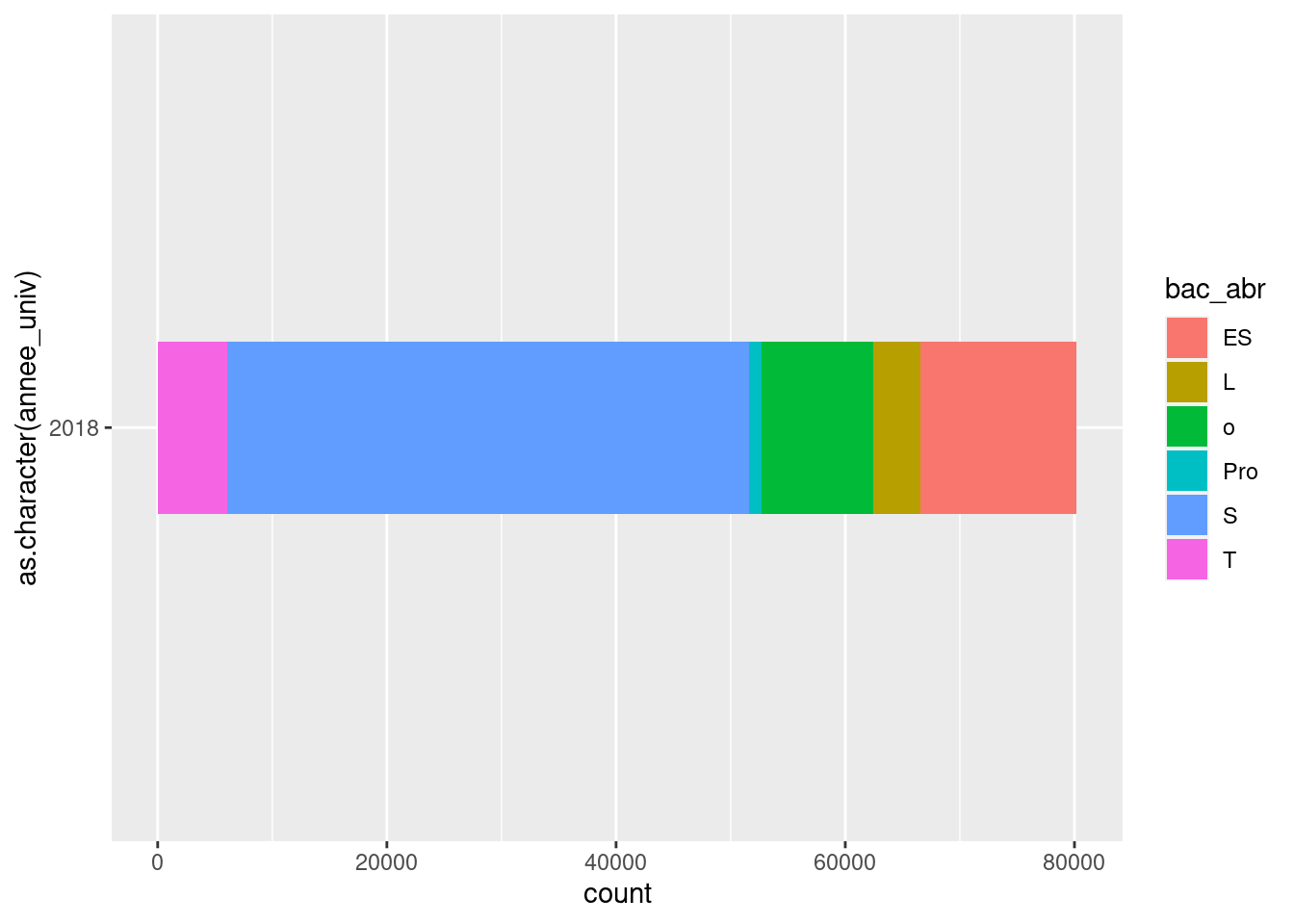
2.4.2 Camemberts et donuts
On peut pousser un peu et étirer le bandeau sur un cercle… afin d’obtenir un
diagramme camembert, qui n’est rien d’autre qu’un diagramme en barre circulaire
! C’est ici qu’intervient la fonction coord_polar(). À noter que l’on n’a ici
plus besoin de déclarer l’année comme chaîne de caractère. Les paramètres
direction change le sens de progression, et permet d’avoir les modalités dans
l’ordre ascendant de la légende :
ggplot(um18, aes(annee_univ, fill = bac_abr)) +
geom_bar() +
coord_polar("y", direction = -1)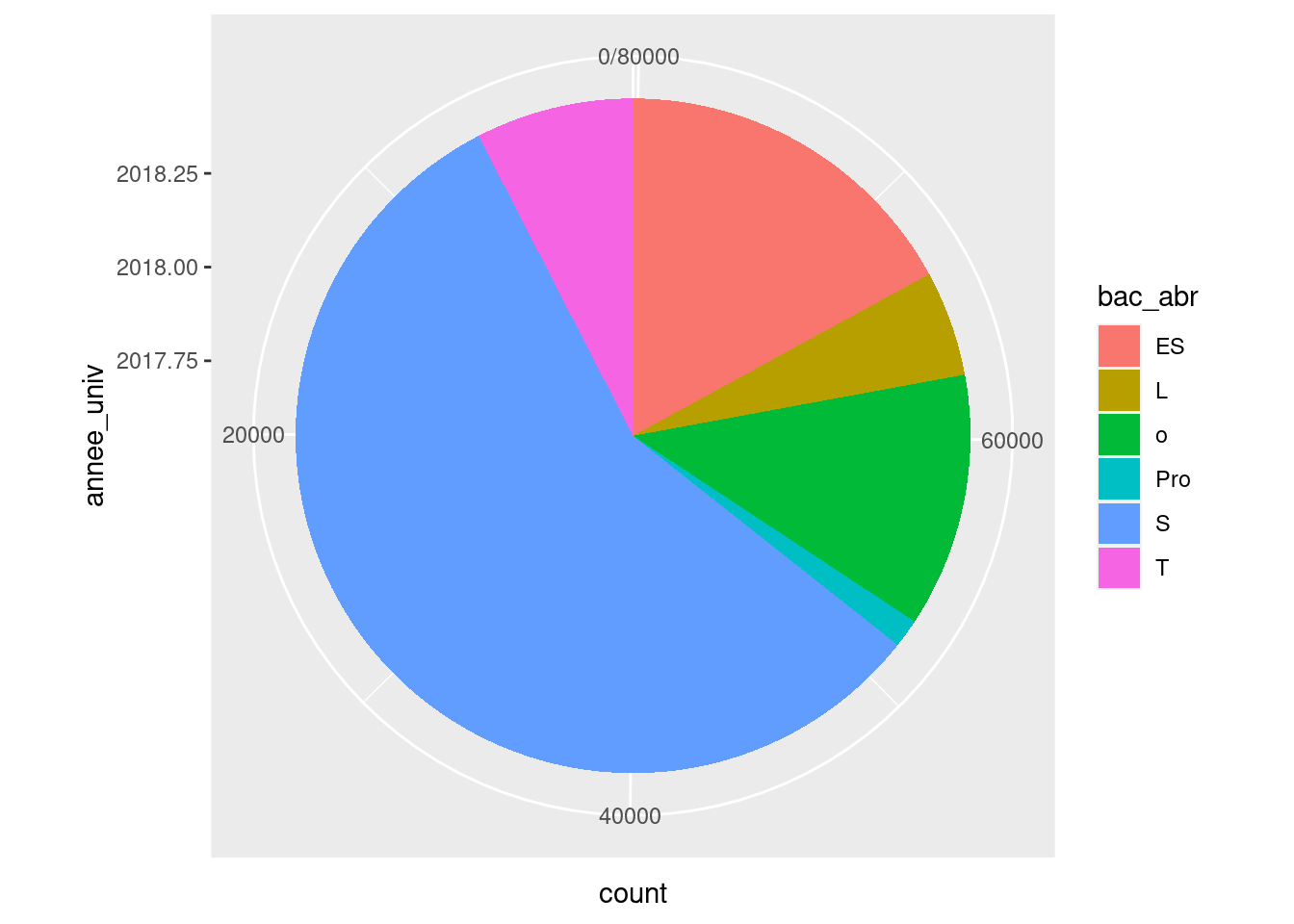
Pour les gourmands qui préfèrent le sucré, ou bien pour diminuer l’impact de la surface du camembert, on pourra opter pour un diagramme donut, qui est simplement un camembert avec un trou. On joue ici sur l’échelle de l’axe des x (l’année universitaire !) :
ggplot(um18, aes(annee_univ, fill = bac_abr)) +
geom_bar() +
coord_polar("y", direction = -1) +
xlim(2016.45, 2018.45)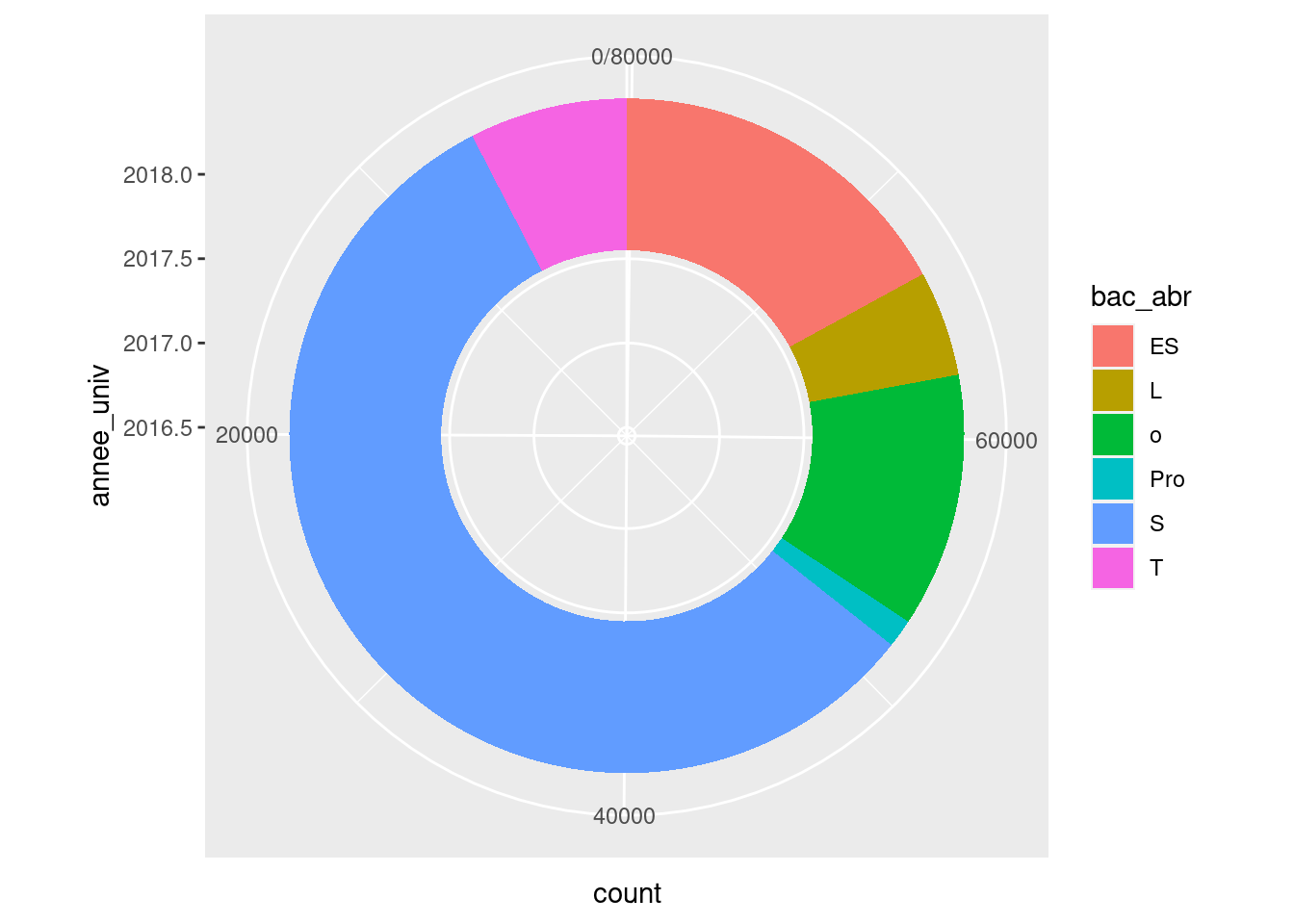
J’introduis ici un exemple complet avec les premiers éléments de style pour
obtenir un résultat plutôt convenable. Après avoir préparé les étiquettes pour
chaque type de bac, on peut supprimer tous les axes et grilles (qui sont
désormais inutiles) avec un thème vide (theme_void()), et on change le nom de
la légende avec labs :
labs <- as.data.frame(rev(table(um18$bac_abr)))
mid <- c(0, cumsum(labs$Freq))
labs$y <- mid[-length(mid)] + diff(mid) / 2
ggplot(um18, aes(annee_univ, fill = bac_abr)) +
geom_bar(color = "white") +
geom_label(data = labs, aes(x = 2018, y = y, label = Var1), inherit.aes = FALSE) +
coord_polar("y", direction = -1) +
xlim(2016.45, 2018.45) +
theme_void() +
labs(fill = "Type de bac")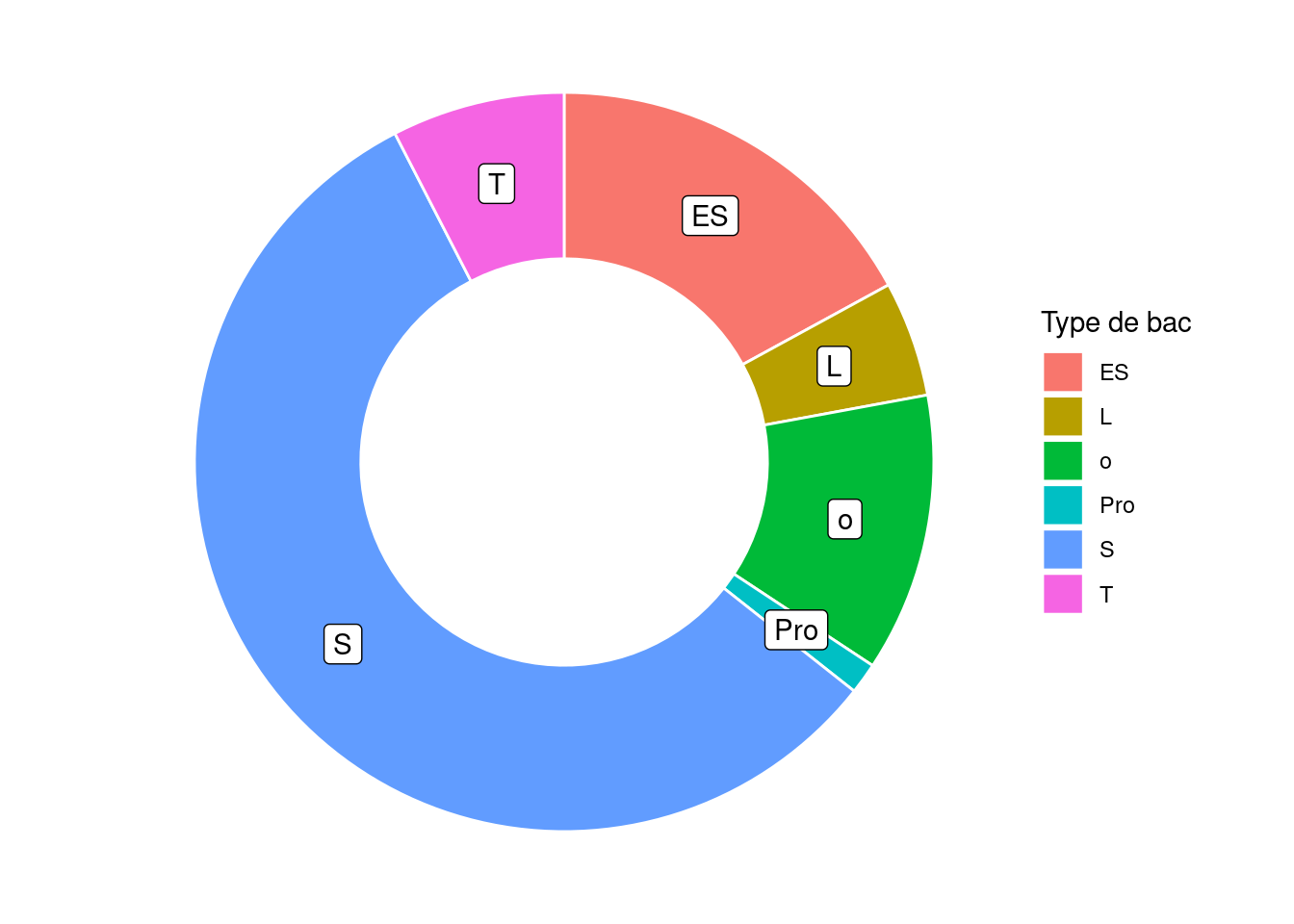
Exercice 1 : Dans cet exercice, on va essayer de se rapprocher au plus près des boîtes à moustache présentées ci-dessous.
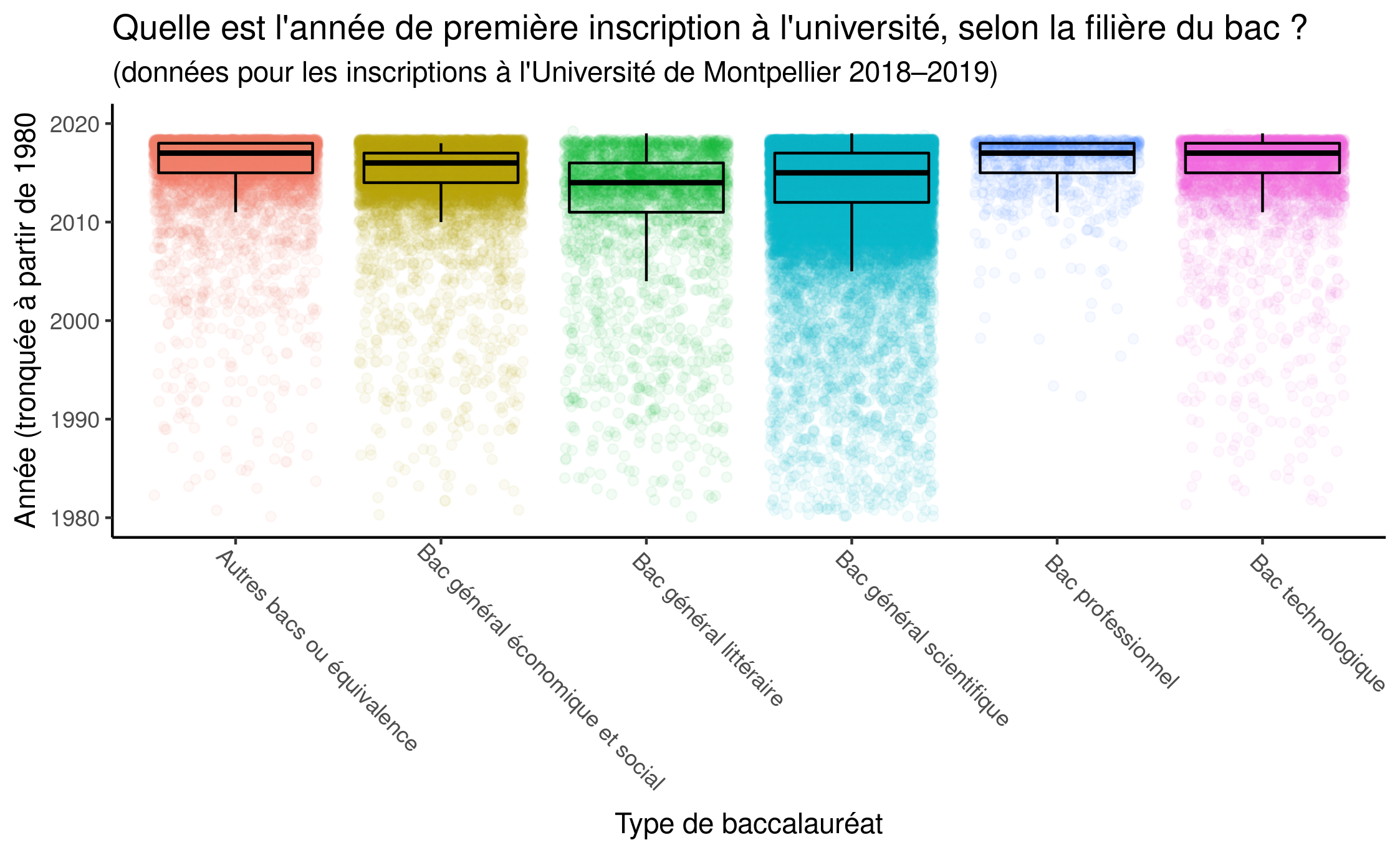
Pour cela, on modifiera les éléments suivants :
-
Données et géométries :
-
On définira un axe de couleurs (
color) selon le type de bac ; -
La géométrie
geom_jitter()permet d’afficher des points en les déplaçant légèrement de manière aléatoire ; -
Les boîtes à moustaches seront transparentes (
alpha) et forcées de couleur noire (color) ;
-
On définira un axe de couleurs (
-
Échelles :
-
Les limites de l’axe des Y seront contraintes entre 1980 et 2000 (
ylim()) ;
-
Les limites de l’axe des Y seront contraintes entre 1980 et 2000 (
-
Décoration :
-
On pourra utiliser le
theme_classic()qui propose une présentation légère ; -
On ajustera tous les titres d’axes et de graphique (
labs()) ; - Pour finir, on pourra enlever la légende et réorienter les modalités sur l’axe des X de 45° vers la droite.
-
On pourra utiliser le
2.4.3 Facettage
Le facettage (faceting) consiste à créer une série de graphiques conditionnels
sur une variable qualitative, ceux-ci étant distribués sur un ruban en deux
dimensions. Le mieux étant de le montrer par l’exemple, plutôt que de regarder
simplement la fréquence des types de bac parmi les inscrits, il serait plus
pertinent de le découper par domaine disciplinaire à l’université. On utilise
pour cela facet_wrap() :
ggplot(um18, aes(bac_abr)) +
geom_bar() +
facet_wrap(vars(domaine_disciplinaire))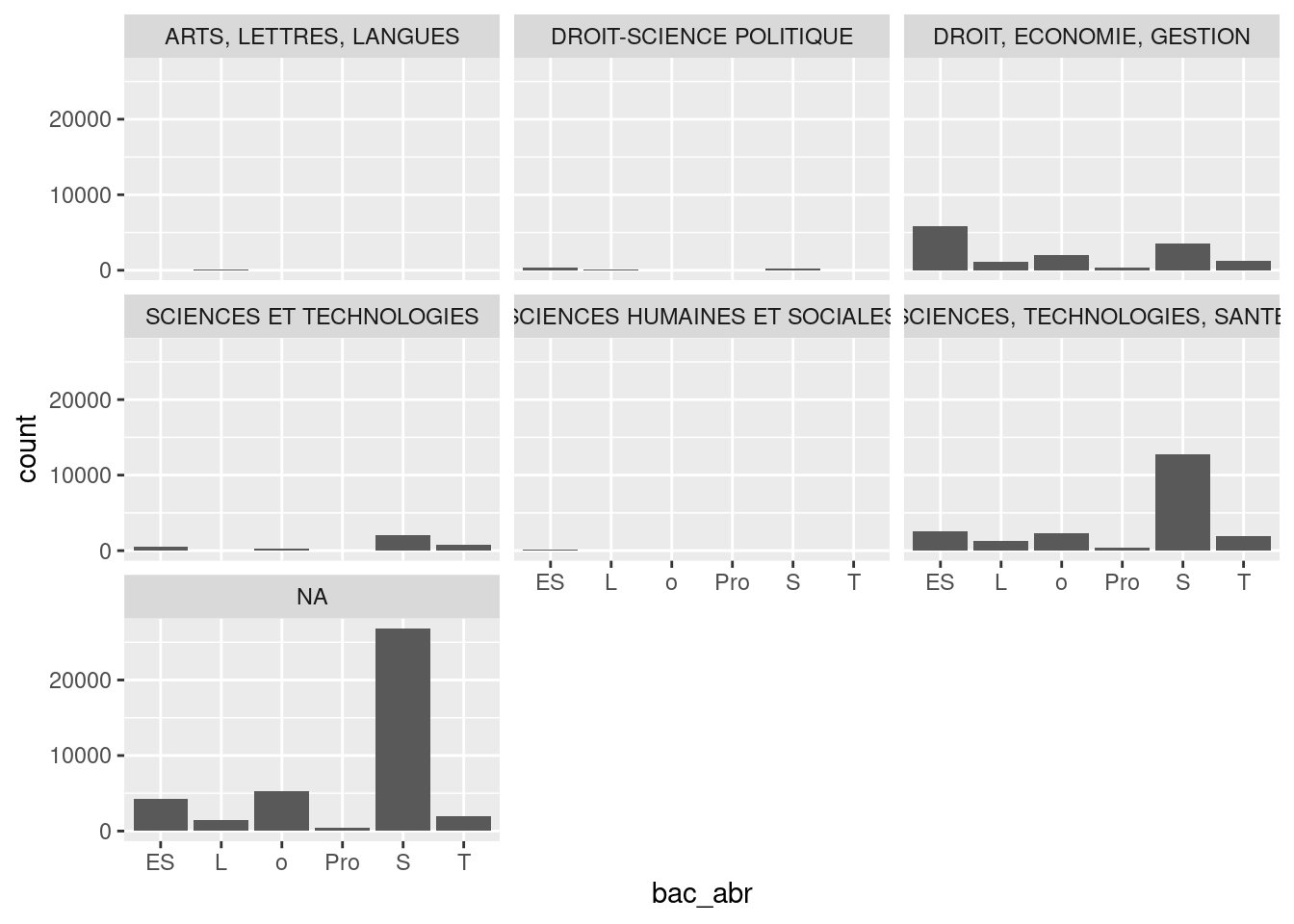
On peut déjà bien voir quelques différences selon les domaines disciplinaires, mais celles-ci sont en grande partie masquées par l’échelle des Y commune à tous les panneaux, et qui écrasent ainsi les domaines à petits effectifs. On peut corriger le problème en utilisant une échelle libre pour chaque panneau :
ggplot(um18, aes(bac_abr)) +
geom_bar() +
facet_wrap(vars(domaine_disciplinaire), scales = "free")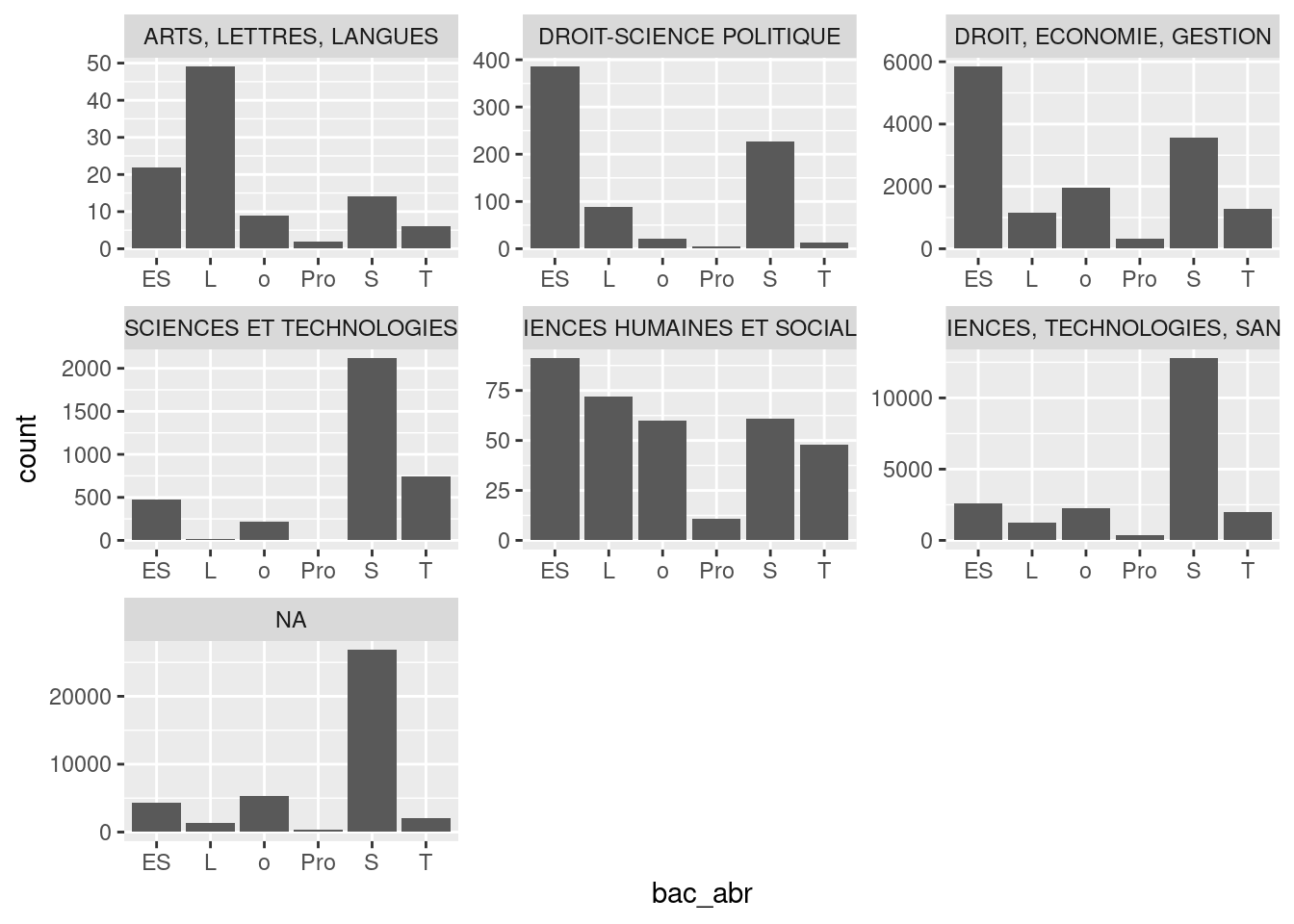
Cette fois, l’origine des étudiants à l’université par domaine disciplinaire est bien plus visible. Le facettage est assez souple et l’on peut par exemple contraindre le nombre de lignes ou de colonnes du ruban :
ggplot(um18, aes(bac_abr)) +
geom_bar() +
facet_wrap(vars(domaine_disciplinaire), scales = "free", nrow = 2)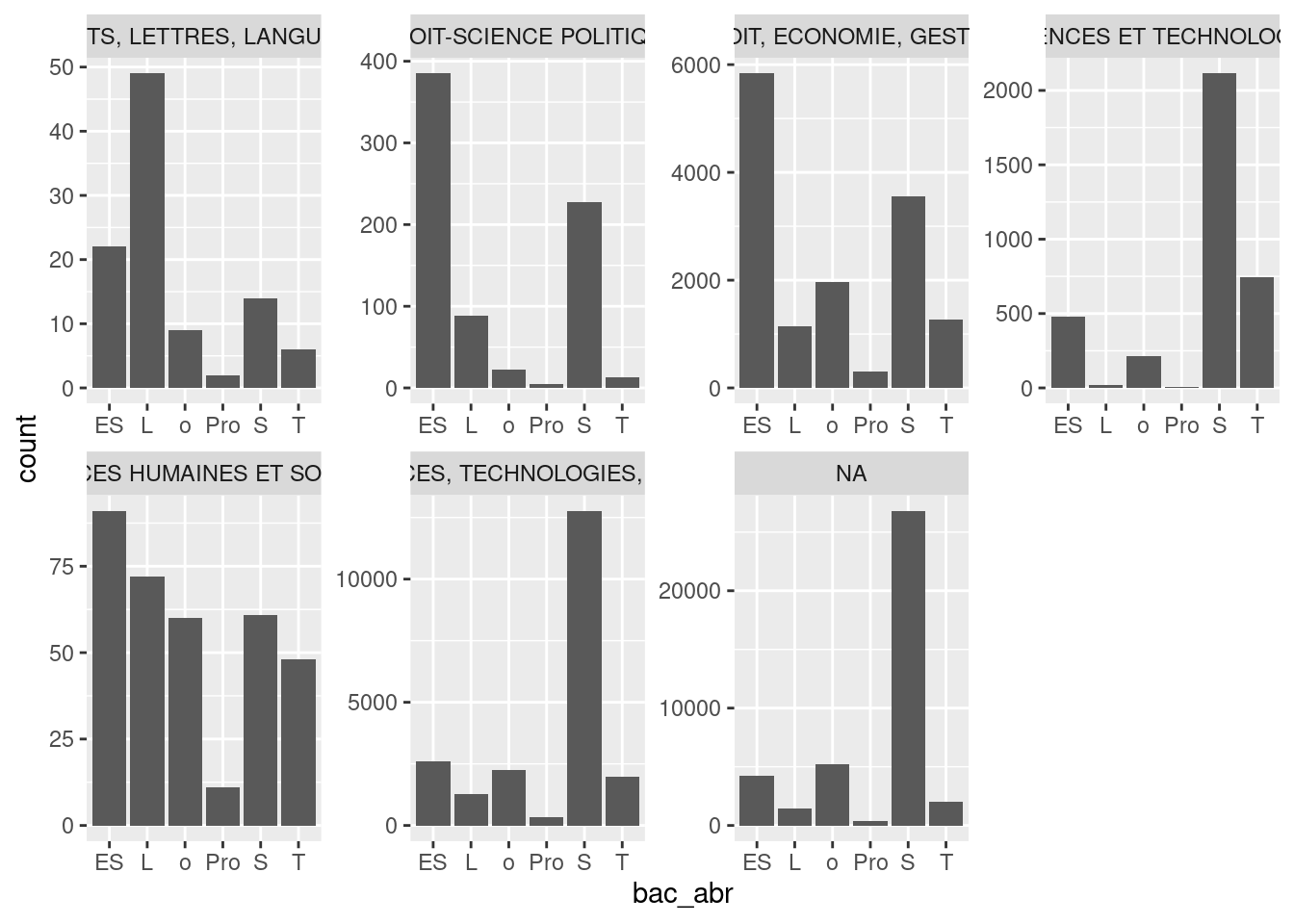
Exercice 2 : Dans cet exercice, on va essayer de se rapprocher au plus près du graphique à multiples panneaux ci-dessous :
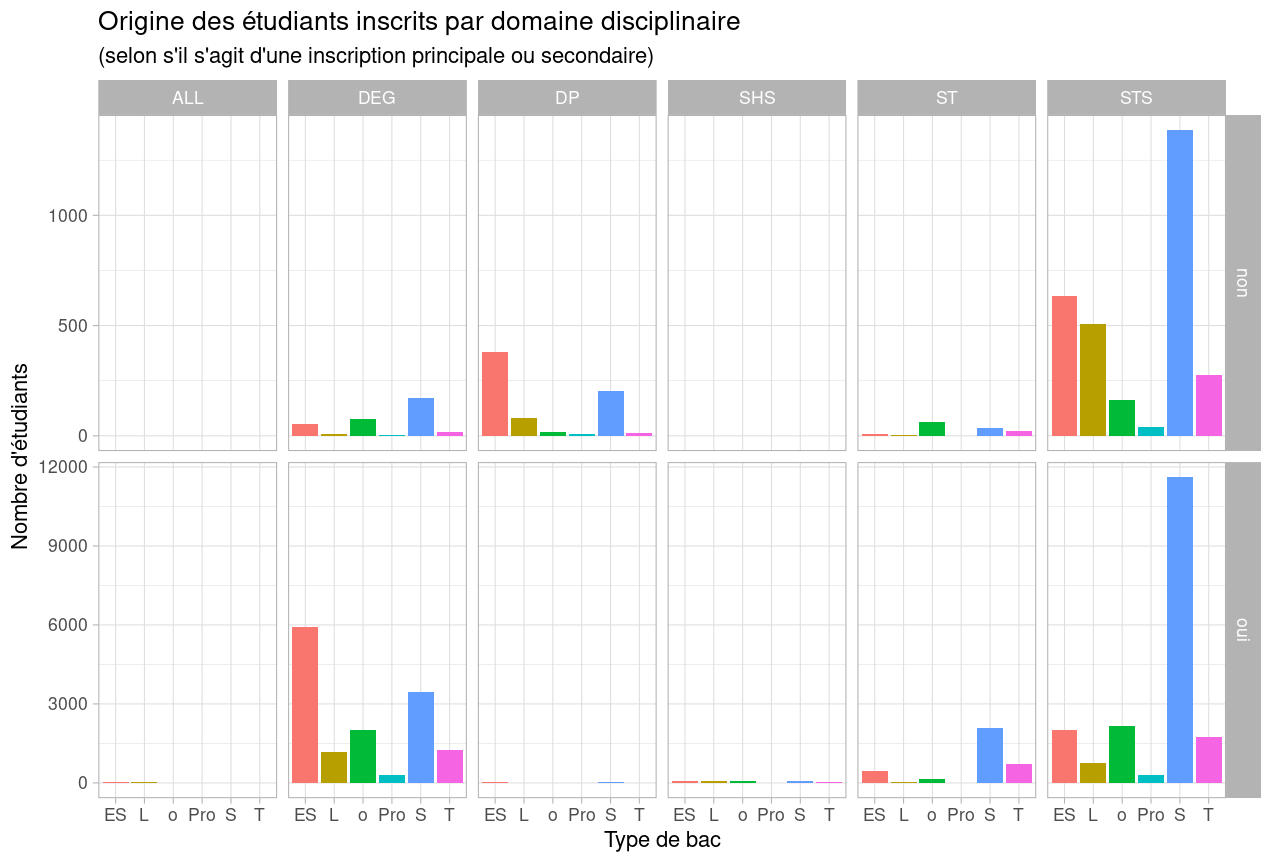
Pour cela, on modifiera les éléments suivants :
-
Données et géométries :
-
On exclura les données manquantes pour le domaine disciplinaire (
is.na()) ; -
On définira un axe de couleurs (
fill) selon le type de bac ;
-
On exclura les données manquantes pour le domaine disciplinaire (
-
Facettage :
-
Pour croiser deux variables, il est plus efficace d’utiliser
facet_grid();
-
Pour croiser deux variables, il est plus efficace d’utiliser
-
Décoration :
-
On pourra utiliser le
theme_light()qui permet de bien comparer les panneaux ; -
On ajustera tous les titres d’axes et de graphique (
labs()) ; - Pour finir, on pourra enlever la légende.
-
On pourra utiliser le
2.5 Sauvegarder / exporter ses graphiques
ggplot2 inclue un mécanisme de sauvegarde des graphiques très simple
d’utilisation et pourtant très puissant. Il permet d’exporter les sorties
graphiques dans à peu près n’importe quel format exploitable en dehors de R, par
exemple les formats PNG pour des images bitmaps (préférable au JPEG, disponible
également), PDF pour une image vectorielle de qualité parfaite, ou encore SVG
pour pouvoir l’éditer ultérieurement dans un logiciel comme Inkscape par
exemple. Chaque format a ses propres avantages et inconvénients, mais surtout
une utilisation bien définie.
Dans son utilisation la plus simple, la fonction ggsave() ne nécessite rien de
particulier et enregistre la dernière sortie graphique en PNG dans un nom de
fichier standardisé. Il est toutefois recommandé de spécifier au minimum le nom
du fichier de sortie (dont l’extension de fichier définit le format) :
ggsave("mon-super-graphique.pdf")On peut également modifier le dossier dans lequel le graphique est exporté, les
dimensions appliquées à la sortie (width et height, par défaut en pouces),
ou encore l’échelle de redimensionnement et la résolution du graphique (scale
et dpi).
Exercice 3 : Votre mission, si vous l’acceptez, enregistrer le dernier graphique en PNG dans le dossier images/, avec une résolution de 150 DPI et un facteur d’échelle de 2. Que constatez-vous ? Vous avez 5 minutes.
