1 Les outils R de base
“A new statistic proves that 73% of all statistics are pure inventions.” — J. J. A. Weber
1.1 Première utilisation
1.1.1 L’environnement R
Sous Windows, quand on lance le logiciel R, on ouvre une fenêtre
spartiate avec une invite de commande dans lequel on peut taper du
code R. Quelques menus sont disponibles, bien qu’ils soient rarement
utilisés. On peut regarder le menu Aide > Console pour trouver un
peu d’aide sur son utilisation…
Il existe une fiche de synthèse pour la syntaxe de base de R, qu’il peut s’avérer très utile de garder sous le coude. Celle-ci est disponible en cliquant sur la vignette ci-dessous (en anglais) :
L’invite de commande, telle une calculatrice, accepte tout type d’arithmétique et fonctions standards :
2+2*15-1[1] 31pi[1] 3.1415931:5[1] 1 2 3 4 5(1:5)^2[1] 1 4 9 16 25sqrt(26)[1] 5.09902rnorm(10) [1] -1.1310088 -0.2094658 1.4061582 -0.5181954 -0.2238918 -1.0626493
[7] -2.4356813 0.3803548 -0.2038204 1.94747141.1.2 RStudio
La présentation avec R étant faite, je recommande désormais vivement d’utiliser RStudio1, un environnement avancé de développement sous R (et accessoirement, Python). RStudio, tout comme R, est un logiciel libre, c’est-à-dire que l’on peut librement et gratuitement le télécharger, l’utiliser et le partager. RStudio fournit une interface complète pour écrire son code R, gérer les données et les sorties graphiques, créer des rapports web, etc.
Commencez par ouvrir le script R (1-r-base.R) avec RStudio. Ce script contient
le code complet pour ce module. Dans fichier de script R, tout ce qui commence
par un dièse # est ignoré, ce sont des commentaires. Tout le reste est du code
R pur jus qui peut donc être exécuté.
Il est important de s’approprier ses outils informatiques autant que possible. RStudio peut apparaître complexe, et présente effectivement de nombreuses fonctionnalités. Pour s’y retrouver, je recommande fortement la fiche de synthèse sur l’interface et les raccourcis claviers, disponible en cliquant sur la vignette ci-dessous (en anglais) :
On retiendra notamment le premier raccourci suivant :
-
Exécuter la ligne courante ou la sélection :
Ctrl+Entrée
Au début d’une session de travail, c’est toujours une bonne idée de vérifier dans quel répertoire de travail R a démarré (normalement son dossier personnel ou bien le dossier du fichier ouvert). Dans RStudio, le répertoire de travail est affiché juste au-dessus de la console. On peut également le retrouver avec :
getwd()Si besoin, il existe plusieurs méthodes pour changer ce dossier — entre autres, la méthode privilégiée en code :
setwd("C:/Documents and Settings/Me/My documents/My folder")1.1.3 Types de données
Sous R, tout est un objet : les données, les sorties, les fonctions,
etc. Pour enregistrer un objet, on utilise la commande d’affectation
<- (Alt+-) :
bla <- 2 + 2
bla[1] 4bla est un vecteur de nombres (numeric) de longueur 1 :
class(bla)[1] "numeric"length(bla)[1] 1Un vecteur peut comporter les nombres que l’on souhaite, qui sont
associés avec la fonction c (for “combine”) :
bla <- c(42, 2 + 2, sqrt(26))
bla[1] 42.00000 4.00000 5.09902class(bla)[1] "numeric"length(bla)[1] 3Les autres types de données les plus communs sont les matrices (matrix), les tableaux (data frame) et les listes (list) :
mat <- matrix(1:20, nrow = 5)
mat [,1] [,2] [,3] [,4]
[1,] 1 6 11 16
[2,] 2 7 12 17
[3,] 3 8 13 18
[4,] 4 9 14 19
[5,] 5 10 15 20df <- data.frame(A = 1:5, B = LETTERS[1:5])
df A B
1 1 A
2 2 B
3 3 C
4 4 D
5 5 Elis <- list(l1 = 1:10, l2 = df, l3 = seq(0, 1, length.out = 5))
lis$l1
[1] 1 2 3 4 5 6 7 8 9 10
$l2
A B
1 1 A
2 2 B
3 3 C
4 4 D
5 5 E
$l3
[1] 0.00 0.25 0.50 0.75 1.00En ce qui concerne les jeux de données, la structure la plus intéressante est en tableaux, avec les observations en lignes, et les variables en colonnes. Un certain nombre de fonctions permettent d’explorer la structure et le contenu de tableaux2. On commence avec un tableau simple avec 20 observations sur 4 variables :
df <- data.frame(
A = rep(c("Petit", "Moyen", "Grand", "Très grand"), each = 5),
B = seq(0, 100, length.out = 20),
C = sample(1:5, 20, replace = TRUE),
D = rnorm(20)
)
head(df) A B C D
1 Petit 0.000000 1 0.006705813
2 Petit 5.263158 5 0.457510669
3 Petit 10.526316 5 0.596220672
4 Petit 15.789474 5 -1.018366805
5 Petit 21.052632 1 0.982404767
6 Moyen 26.315789 2 -0.817914806tail(df) A B C D
15 Grand 73.68421 4 0.7780805
16 Très grand 78.94737 1 0.9090837
17 Très grand 84.21053 2 0.4363311
18 Très grand 89.47368 5 1.1641237
19 Très grand 94.73684 1 -2.1628477
20 Très grand 100.00000 2 -0.7847279str(df)'data.frame': 20 obs. of 4 variables:
$ A: chr "Petit" "Petit" "Petit" "Petit" ...
$ B: num 0 5.26 10.53 15.79 21.05 ...
$ C: int 1 5 5 5 1 2 3 4 5 5 ...
$ D: num 0.00671 0.45751 0.59622 -1.01837 0.9824 ...summary(df) A B C D
Length:20 Min. : 0 Min. :1.00 Min. :-2.1628
Class :character 1st Qu.: 25 1st Qu.:1.75 1st Qu.:-0.8097
Mode :character Median : 50 Median :2.50 Median : 0.1458
Mean : 50 Mean :3.05 Mean :-0.1300
3rd Qu.: 75 3rd Qu.:5.00 3rd Qu.: 0.5637
Max. :100 Max. :5.00 Max. : 1.1641 names(df)[1] "A" "B" "C" "D"dim(df)[1] 20 4table(df$C)
1 2 3 4 5
5 5 1 2 7 table(df$A, df$C)
1 2 3 4 5
Grand 1 2 0 1 1
Moyen 0 1 1 1 2
Petit 2 0 0 0 3
Très grand 2 2 0 0 1Finalement, on peut aussi écrire ses propres fonctions, plus ou moins complexes, et les enregistrer comme tout autre objet :
racine <- function(x)
{
paste("La racine carrée de", x, "est", sqrt(x))
}
racine(2)[1] "La racine carrée de 2 est 1.4142135623731"Tous les objets sont enregistrés dans l’environnement de
l’utilisateur, qui n’existe que le temps de la session, c’est-à-dire
tant que R est ouvert. Il est possible de lister les objets (ls()),
de les supprimer de l’environnement (rm() pour remove), ou bien
même de sauvegarder l’environnement complet pour une utilisation
ultérieure (save.image())3 :
ls()[1] "bla" "df" "lis" "mat" "racine"rm(mat)
ls()
save.image(file = "Session.RData")1.1.4 Besoin d’aide ?
R propose plusieurs moyens de trouver les réponses à ses questions (à ce niveau, il faut se rappeler que R est un logiciel développé en anglais) :
help("sqrt")
?sqrt
apropos("test")
help.search("linear model")help et ? sont deux fonctions équivalentes pour accéder à la
documentation d’une fonction précise. La documentation R est par
construction complète (tous les arguments sont listés et détaillés,
les sorties sont expliquées, et chaque fonction est assortie
d’exemples directement fonctionnels) mais également légèrement
absconse. En particulier, la documentation n’est pas là pour apprendre
les statistiques ou les modèles derrière les fonctions, c’est une
documentation résolument technique. Par ailleurs, apropos liste
toutes les fonctions qui contiennent le mot recherché dans le nom-même
de la fonction, et help.search fait une recherche complète dans la
documentation R des termes renseignés.
Pour finir, les meilleures ressources pour trouver de l’information ou de l’aide pour R sont en ligne. La communauté R est incroyablement dynamique, diverse et réactive, que ce soit des développeurs ou bien d’autres utilisateurs. La source en ligne la plus notable pour ce qui concerne les problèmes sous R est actuellement Stack Overflow, un forum ouvert « aux développeurs pour apprendre, partager leurs connaissances, et construire leurs carrières ». Concernant la « science des données », Hadley Wickham propose en libre accès [un livre fantastique](https://r4ds.had.co.nz/ couvrant bien plus en détails tous les aspects couverts par les JPA-R (en anglais).
sphere, qui retourne, à partir d’un rayon
donné, l’aire de la sphère correspondante (de formule \(A = 4\pi r^2\)),
son volume (\(V = \frac{4\pi r^3}{3}\)), et sa compacité
(\(C = \frac{V}{A} = \frac{r}{3}\)).
1.2 La variance des iris

Figure 1.1: Les iris de Fisher et Anderson.
1.2.1 Présentation
Partons désormais du côté d’un des jeux de données statistiques les
plus célèbres : les iris de Fisher (et Anderson). Ce jeu de donnée est
livré avec R, et est directement disponible dans l’object
iris. Regardons de quoi il en retourne :
class(iris)[1] "data.frame"head(iris) Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosastr(iris)'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...Ce jeu de données présente les mesures effectuées sur un total de 150 fleurs d’iris de trois espèces différentes (exactement 50 fleurs par espèce) :
table(iris$Species)
setosa versicolor virginica
50 50 50 On peut d’ores et déjà vérifier que la taille des pétales augmente avec la taille des sépales, ce que l’on pouvait intuitivement deviner :
plot(x = iris$Sepal.Length, y = iris$Petal.Length)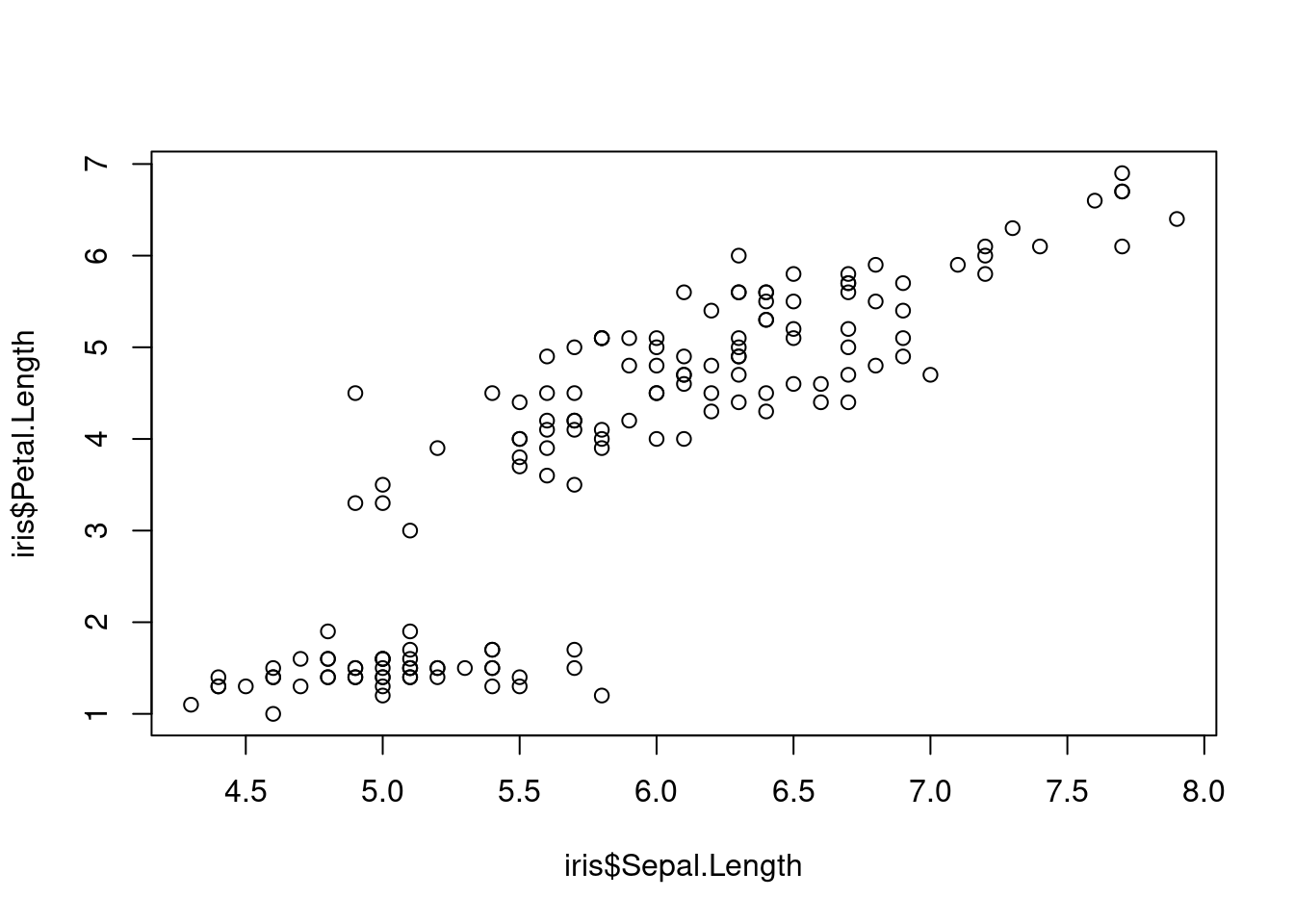
Figure 1.2: Longueur des pétales vs. sépales.
La fonction plot est assez basique à utiliser, elle nécessite de
renseigner la variable en x et la variable en y. Elle accepte
également une « formule », c’est-à-dire une expression de la forme y ~ x (variable expliquée en fonction de variables explicatives). Les
formules sont largement utilisées en statistiques sous R, notamment
pour la spécification des modèles, par exemple les modèles linéaires :
plot(iris$Petal.Length ~ iris$Sepal.Length)
abline(lm(iris$Petal.Length ~ iris$Sepal.Length))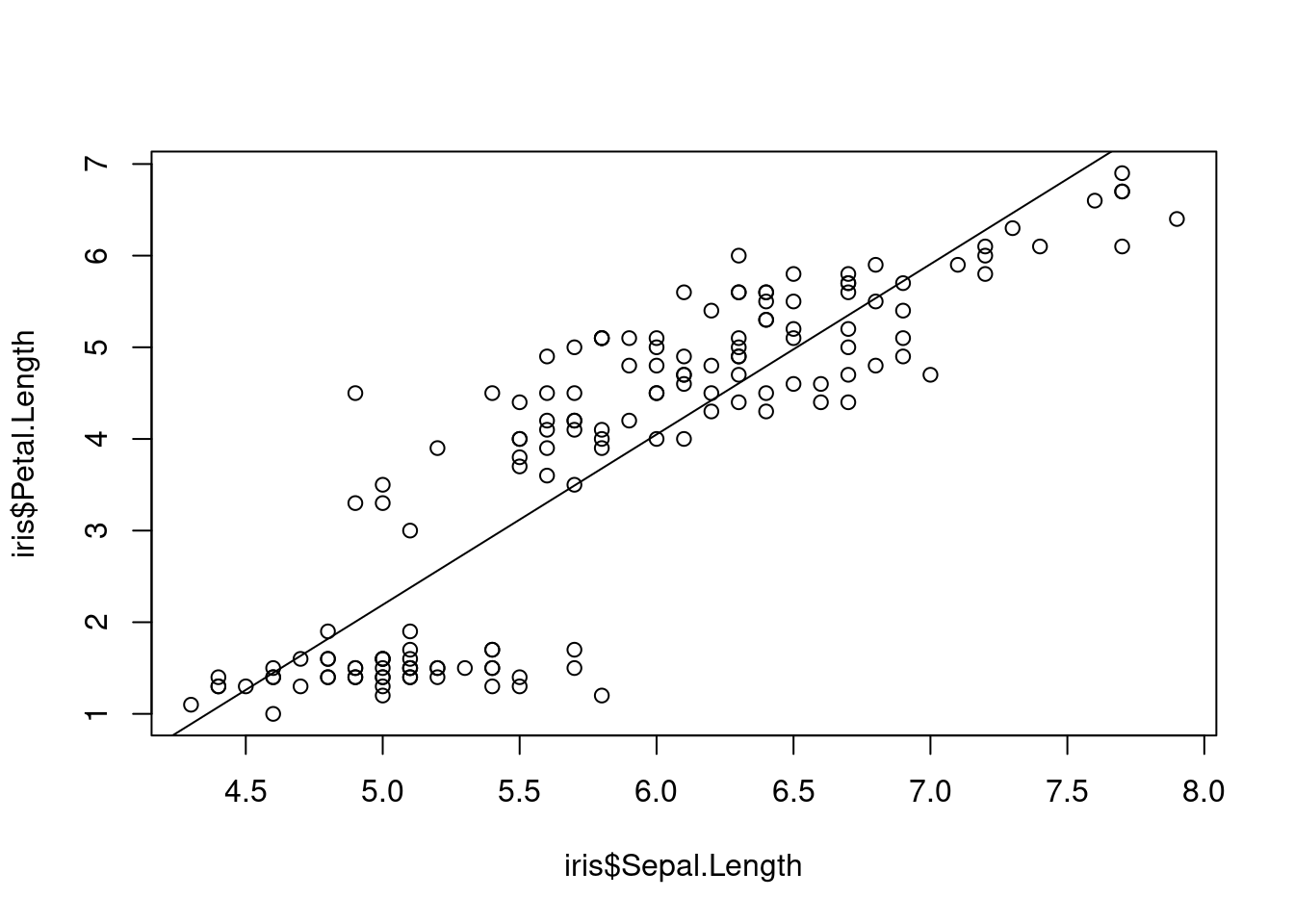
Figure 1.3: Longueur des pétales vs. sépales, avec modèle linéaire.
Mais est-ce que la figure n’est pas un peu trompeuse ? Rappelons-nous qu’il y a trois espèces différentes, voyons voir comment celles-ci se comparent :
plot(iris$Petal.Length ~ iris$Sepal.Length, col = as.numeric(iris$Species))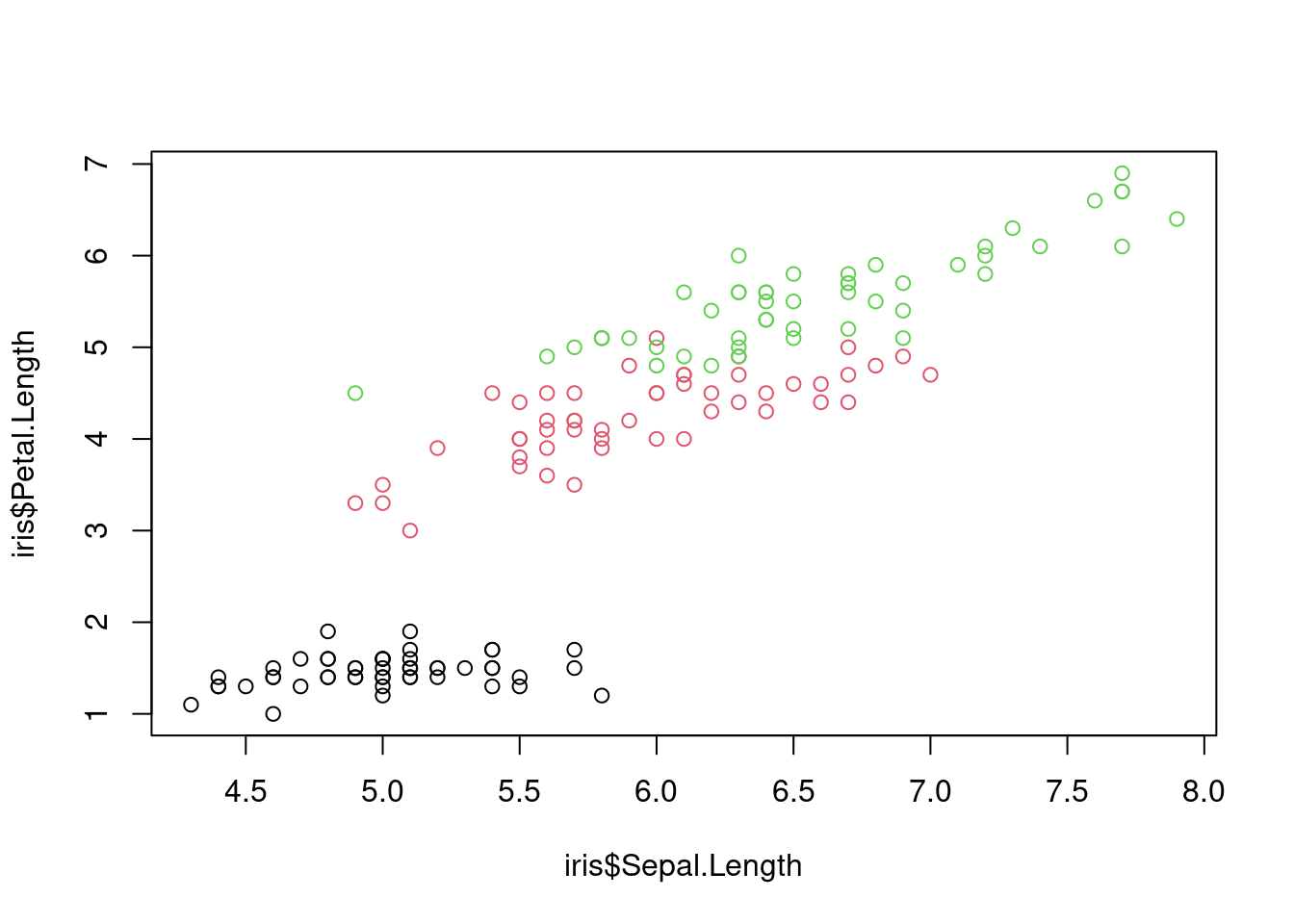
Figure 1.4: Longueur des pétales vs. sépales, couleur par espèce.
On commence à y entrevoir quelques tendances… que l’on peut
distinctement voir en séparant les trois espèces avec la fonction
coplot (“conditioning plots”). Cette fonction introduit la barre
verticale (“pipe”) comme opérateur conditionnel :
coplot(iris$Petal.Length ~ iris$Sepal.Length | iris$Species, columns = 3)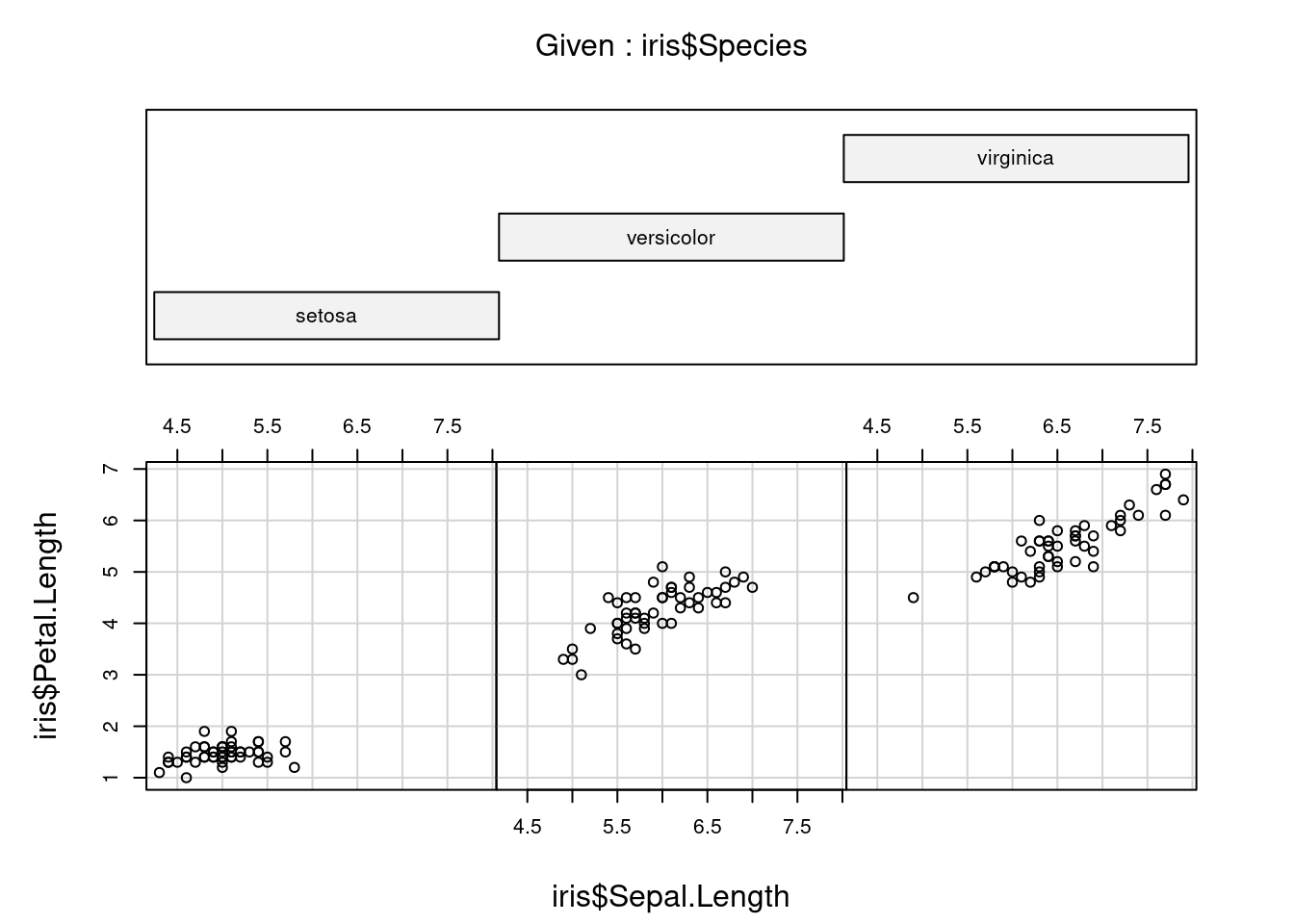
Figure 1.5: Longueur des pétales vs. sépales, par espèce.
1.2.2 Comparaison de moyennes
Regardons désormais la largeur des pétales. Est-ce que celle-ci varie par espèce ?
boxplot(iris$Petal.Width ~ iris$Species)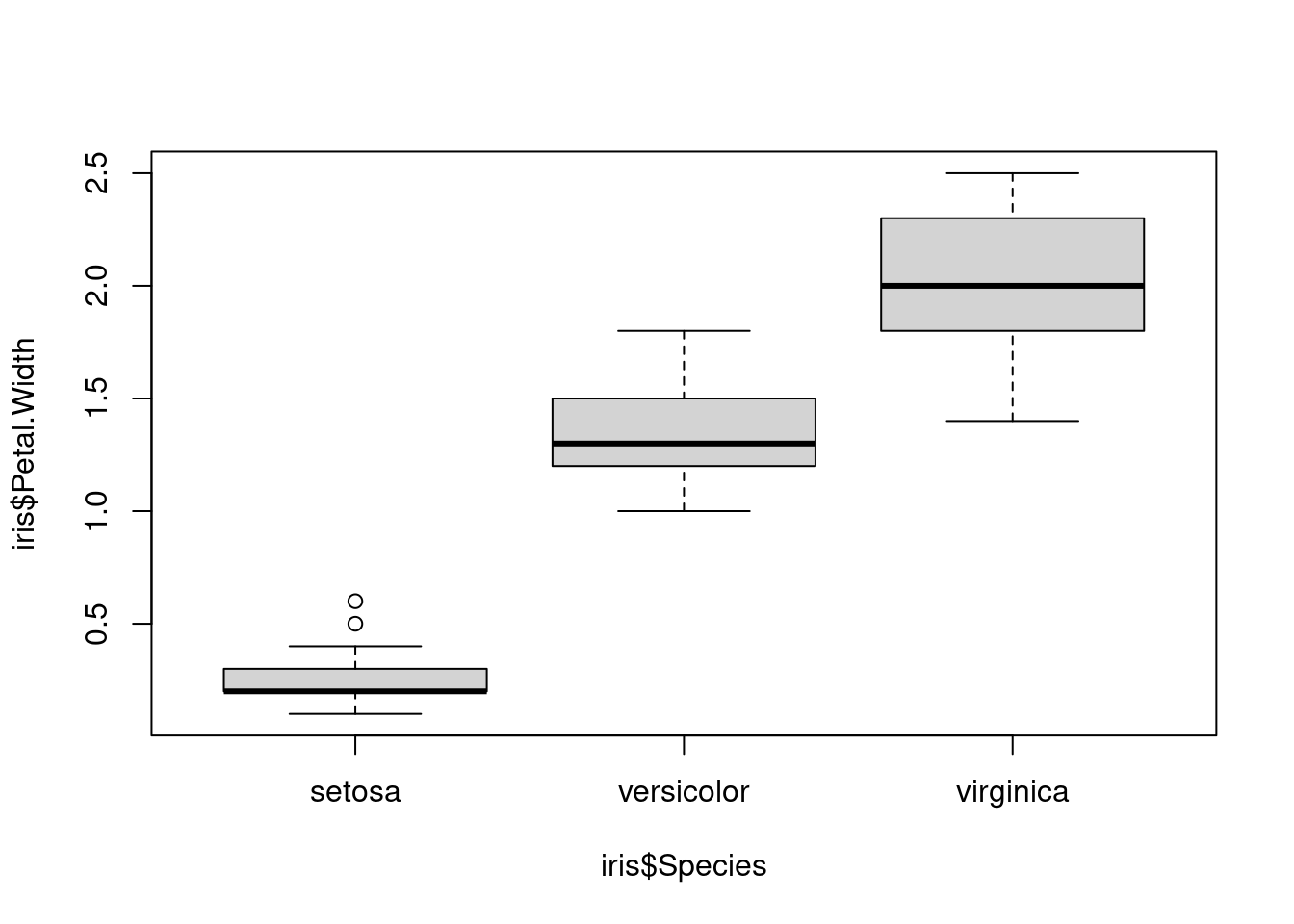
Figure 1.6: Largeur des pétales, par espèce.
Il semble en effet y avoir de larges différences. Nous allons maintenant les quantifier et finalement les tester :
mean(iris$Petal.Width[iris$Species == "setosa"])[1] 0.246by(iris$Petal.Width, iris$Species, mean)iris$Species: setosa
[1] 0.246
------------------------------------------------------------
iris$Species: versicolor
[1] 1.326
------------------------------------------------------------
iris$Species: virginica
[1] 2.026Sur la base de ces valeurs, on pourrait effectivement penser qu’il y a une différence nette. Une première approche serait de comparer les espèces deux par deux à l’aide de tests t de Student :
t.test(iris$Petal.Width[iris$Species == "setosa"],
iris$Petal.Width[iris$Species == "versicolor"])
Welch Two Sample t-test
data: iris$Petal.Width[iris$Species == "setosa"] and iris$Petal.Width[iris$Species == "versicolor"]
t = -34.08, df = 74.755, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-1.143133 -1.016867
sample estimates:
mean of x mean of y
0.246 1.326 t.test(iris$Petal.Width[iris$Species == "setosa"],
iris$Petal.Width[iris$Species == "virginica"])
Welch Two Sample t-test
data: iris$Petal.Width[iris$Species == "setosa"] and iris$Petal.Width[iris$Species == "virginica"]
t = -42.786, df = 63.123, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-1.863133 -1.696867
sample estimates:
mean of x mean of y
0.246 2.026 t.test(iris$Petal.Width[iris$Species == "versicolor"],
iris$Petal.Width[iris$Species == "virginica"])
Welch Two Sample t-test
data: iris$Petal.Width[iris$Species == "versicolor"] and iris$Petal.Width[iris$Species == "virginica"]
t = -14.625, df = 89.043, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.7951002 -0.6048998
sample estimates:
mean of x mean of y
1.326 2.026 Toutes les différences sont significatives… mais l’approche est biaisée par la multiplication des tests, ce qui multiplie d’autant le risque d’erreur (par exemple, si nous avions 10 classes, nous aurions besoin d’effectuer 45 tests !). C’est pourquoi nous avons besoin d’une analyse de la variance (ANOVA) qui permet d’appréhender ce problème de comparaison de moyenne en un seul test.
1.2.3 Analyse de la variance (ANOVA)
Il existe une première fonction dédiée à l’analyse de variance :
aov, qui effectue une décomposition de la variance et retourne les
sommes des carrés des écarts (SCEs) inter (modèle) et intra
(résiduelle) :
aov(iris$Petal.Width ~ iris$Species)Call:
aov(formula = iris$Petal.Width ~ iris$Species)
Terms:
iris$Species Residuals
Sum of Squares 80.41333 6.15660
Deg. of Freedom 2 147
Residual standard error: 0.20465
Estimated effects may be unbalancedLe test lui-même est réalisé par la fonction anova, basée sur le
modèle linéaire que nous voulons ajuster :
anova(lm(iris$Petal.Width ~ iris$Species))Analysis of Variance Table
Response: iris$Petal.Width
Df Sum Sq Mean Sq F value Pr(>F)
iris$Species 2 80.413 40.207 960.01 < 2.2e-16 ***
Residuals 147 6.157 0.042
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Il y a donc bien une différence entre les moyennes : la taille des pétales varie de manière marquée entre espèces d’iris.
Exercice 2 : Dans cet exercice, l’objectif est d’arriver au résultat du test d’ANOVA manuellement, en plusieurs étapes :
Calculer la moyenne globale des largeurs de pétales d’iris, ainsi que les moyennes par espèces.
Calculer les SCEs totale (\(SCE_T = \sum_{i,j} (y_{ij} - \overline{y})^2\)), inter (\(SCE_M = \sum_{i,j} (\overline{y_{i}} - \overline{y})^2\)) et intra (\(SCE_R = \sum_{i,j} (y_{ij} - \overline{y_i})^2\)). Les comparer aux sorties précédentes.
Calculer la valeur de F (\(\mathcal{F} = \frac{SCE_M / \scriptstyle{k-1}}{SCE_R / \scriptstyle{n-k}}\)), et finalement la valeur de p du test d’ANOVA.
Calculer le rapport d’explication \(\eta^2\), c’est-à-dire la proportion de la variance inter dans la variance totale.
1.3 Addendum technique : la gestion de fichiers et de projets
1.3.1 Gestion de projets sous R
Très rapidement sous R, on doit apprendre à organiser ses scripts et ses données. Sur la base de mon expérience, je propose de suivre les règles suivantes :
- Une étude est un projet en soi : tout ce qui la concerne doit se trouver au sein d’un même dossier avec un nom explicite.
- On évite au possible les espaces dans les noms de fichiers et de dossiers.
- Dans un projet (donc un dossier), on trie les fichiers selon leur nature :
- Les scripts R (fichiers
.Rou.Rmd) sont placés à la racine du dossier. - Les fichiers de données (Excel, CSV, etc.) sont placés dans un sous-dossier
data. - Les images, que ce soit des documents ou bien des graphiques exportés, sont
placés dans un sous-dossier
images. - Les sorties R (par exemple des documents PDF ou web comme nous le verrons
dans le dernier module) sont placés dans un sous-dossier
output. - D’autres sous-dossiers peuvent être créés au besoin.
- Les scripts R (fichiers
projet
├── data/
├── images/
├── output/
├── script1.R
├── script2.R
├── fichier1.Rmd
└── fichier2.RmdÀ partir de cette organisation, RStudio permet de gérer des projets de manière
plus fluide, notamment afin de ne pas se perdre avec le répertoire de travail de
R. Pour cela, vous aller tout de suite créer un projet avec le bouton qui va
bien (Create a project). Nous partons d’un dossier existant (Existing
Directory), qu’il faut rechercher manuellement s’il n’apparaît pas
automatiquement. RStudio est immédiatement rechargé en utilisant ce dossier
comme base de travail ; on peut par exemple le voir dans l’onglet d’exploration
de fichiers (Files en bas à droite). Un fichier JPAR-2021.Rproj est
également créé dans votre dossier de travail, il vous permettra de rouvrir le
projet dans l’état où vous l’avez laissé en fermant RStudio. Ce que vous pouvez
d’ailleurs faire maintenant pour tester avant de rouvrir le projet directement.
1.3.2 Les fichiers .R et .Rmd
Les fichiers de script R (fichiers .R) contiennent essentiellement du code R,
qui n’est pas nécessairement reproductible ou complet. On peut y ajouter des
commentaires (tout ce qui est après un dièse #).
À partir de maintenant, nous n’allons plus travailler sur des fichiers de
scripts R mais sur des fichiers R Markdown (.Rmd). R Markdown permet de
produire des analyses reproductibles documentées : on y trouve à la fois des
explications (qui peuvent être aussi détaillées que possible) et des blocs de
code R classique (ouverts et fermés par ```). Un fichier R Markdown permet
de focaliser l’attention sur ce qu’on fait (documentation et explications) et
non sur le « comment » (code R). Il permet également de s’assurer d’avoir du
code reproductible, ce qui est un avantage non négligeable sur le long terme.
Nous verrons plus en détails comment créer et utiliser les fichiers R Markdown dans le dernier module de la formation. En attendant, nous pouvons déjà rajouter deux nouveaux raccourcis dans notre liste :
- Exécuter un bloc de code R en entier :
Ctrl+Shift+Entrée - Ajouter un bloc de code R :
Ctrl+Alt+I
Finalement, un fichier R Notebook (.Rmd également) est une extension du R
Markdown, qui ajoute la possibilié de prévisualiser les résultats au fur et à
mesure, et de coder de manière itérative plus facilement. À tester !
1.3.3 Les fichiers .RData
Il peut parfois être utile de sauvegarder des objets R (fonction save()).
Ceux-ci peuvent alors être chargés très rapidement en l’état dans une session R
(fonction load()), ce qui permet par exemple de les réutiliser dans d’autres
scripts, ou bien de partager des données de manière plus portable (mais en
perdant sur la compatibilité de formats puisque les fichiers .RData ne sont
lisibles que sous R).
La syntaxe pour sauvegarder un objet R est on ne peut plus simple :
save(mon_objet, file = "mon_fichier.RData")Pour charger, c’est encore plus simple :
load("mon_fichier.RData")Par exemple, on va charger les données d’inscription à l’Université de
Montpellier (année 2018–2019), qui seront utilisées pour les modules
suivants. Les données des étudiants impliquent plusieurs étapes et de nombreuses
lignes de code — que nous allons détailler ensuite dans les prochains
modules. Pour aller plus vite, j’ai sauvegardé le jeu de données final um18
dans le fichier data/um18.RData que l’on peut charger directement :
load("data/um18.RData")
um18[1:5, 1:7] decede annee_univ idetu civilite date_naiss code departement_pays
1 non 2018 1035789 Mme 2000-10-05 84 VAUCLUSE
2 non 2018 2211839 M 1997-06-16 6 ALPES MARITIMES
3 non 2018 2211840 M 2000-04-13 84 VAUCLUSE
4 non 2018 921768 Mme 1993-10-08 205 LIBAN
5 non 2018 921685 Mme 1994-10-02 352 ALGERIEclass(um18)[1] "tbl_df" "tbl" "data.frame"dim(um18)[1] 80188 106Que l’on peut télécharger ici : https://rstudio.com/products/rstudio/↩︎
En réalité, toutes ces fonctions peuvent être utilisées sur tout type de données, mais ne seront montrées ici que sur les tableaux. N’hésitez pas à les essayer sur d’autres types de données !↩︎
L’action par défaut quand l’on quitte R est de demander à l’utilisateur s’il souhaite sauvegarder son environnement dans un fichier
.RData.↩︎

