3 Érable de Montpellier (Acer monspessulanum)
On recommence la même chose pour l’érable de Montpellier, espèce méditerranéenne commune.
3.1 Taxonomie
On vérifie le statut taxonomique de l’érable de Montpellier sur l’ossature de taxonomie du GBIF :
[1] "Acer monspessulanum"# A tibble: 1 × 7
scientificName status synonym species speciesKey confidence matchType
<chr> <chr> <lgl> <chr> <int> <int> <chr>
1 Acer monspessulanum L. ACCEPTED FALSE Acer monspessulanum 7262958 99 EXACT Pour l’érable de Montpellier, rien à signaler, c’est directement le nom scientifique accepté.
3.2 Données d’occurrences GBIF
Collecte des données du GBIF :
<<gbif download metadata>>
Status: SUCCEEDED
DOI: 10.15468/dl.b4gmmf
Format: SIMPLE_CSV
Download key: 0145398-230224095556074
Created: 2023-04-05T14:46:09.921+00:00
Modified: 2023-04-05T14:47:44.249+00:00
Download link: https://api.gbif.org/v1/occurrence/download/request/0145398-230224095556074.zip
Total records: 27501On peut dès lors explorer rapidement les données (classe du jeu de données et premières lignes du tableau) :
# A tibble: 27,501 × 50
gbifID datasetKey occurrenceID kingdom phylum class order family genus species
* <int64> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr>
1 4.61e-315 38b4c89f-584c-41bb-bd8f-cd1de… "urn:lsid:a… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
2 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
3 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
4 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
5 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
6 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
7 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
8 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
9 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
10 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
# ℹ 27,491 more rows
# ℹ 40 more variables: infraspecificEpithet <chr>, taxonRank <chr>, scientificName <chr>,
# verbatimScientificName <chr>, verbatimScientificNameAuthorship <chr>, countryCode <chr>,
# locality <chr>, stateProvince <chr>, occurrenceStatus <chr>, individualCount <int>,
# publishingOrgKey <chr>, decimalLatitude <dbl>, decimalLongitude <dbl>,
# coordinateUncertaintyInMeters <dbl>, coordinatePrecision <dbl>, elevation <dbl>,
# elevationAccuracy <dbl>, depth <dbl>, depthAccuracy <dbl>, eventDate <dttm>, day <int>, …Puis les transformer en objets géographiques (format Simple feature de sf) :
Simple feature collection with 27501 features and 50 fields
Attribute-geometry relationship: 50 constant, 0 aggregate, 0 identity
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -123.298889 ymin: -43.586 xmax: 172.09 ymax: 59.9172
Geodetic CRS: WGS 84
# A tibble: 27,501 × 51
gbifID datasetKey occurrenceID kingdom phylum class order family genus species
* <int64> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr>
1 4.61e-315 38b4c89f-584c-41bb-bd8f-cd1de… "urn:lsid:a… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
2 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
3 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
4 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
5 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
6 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
7 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
8 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
9 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
10 4.55e-315 6ac3f774-d9fb-4796-b3e9-92bf6… "" Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
# ℹ 27,491 more rows
# ℹ 41 more variables: infraspecificEpithet <chr>, taxonRank <chr>, scientificName <chr>,
# verbatimScientificName <chr>, verbatimScientificNameAuthorship <chr>, countryCode <chr>,
# locality <chr>, stateProvince <chr>, occurrenceStatus <chr>, individualCount <int>,
# publishingOrgKey <chr>, decimalLatitude <dbl>, decimalLongitude <dbl>,
# coordinateUncertaintyInMeters <dbl>, coordinatePrecision <dbl>, elevation <dbl>,
# elevationAccuracy <dbl>, depth <dbl>, depthAccuracy <dbl>, eventDate <dttm>, day <int>, …Il y a 27 501 occurrences dans le jeu de données. On les affiche sur la carte du monde :
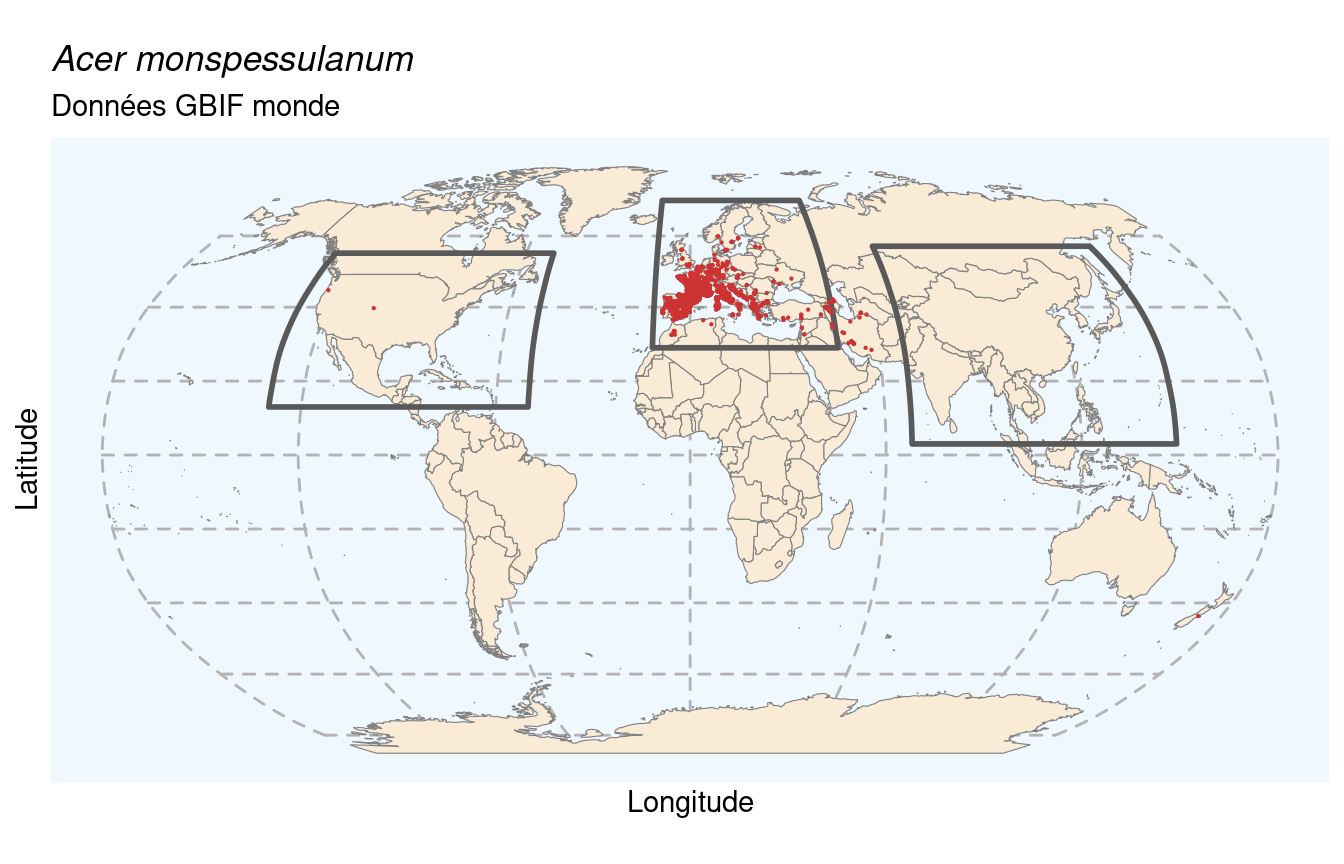
Figure 3.1: Occurrences de Acer monspessulanum dans le monde.
3.3 Données par région
On évalue la proportion d’occurrences dans chaque région, en utilisant les 3 masques créés précédemment. Si on a au moins 50 % des occurrences dans une région, on peut continuer en travaillant uniquement sur ces données. Sinon, on vérifie qu’au moins 67 % des données tombent dans l’ensemble des régions, et on prend la région la plus représentée. Au final, s’il s’agit d’une espèce endémique d’Europe, on n’a pas besoin de manipulation supplémentaire.
[1] 0.9989454929[1] 7.27246282e-05[1] 0On obtient 99.89 % d’occurrences en Europe, on est bien sur une espèce endémique de la région. On peut récupérer les données d’Europe, et les cartographier :
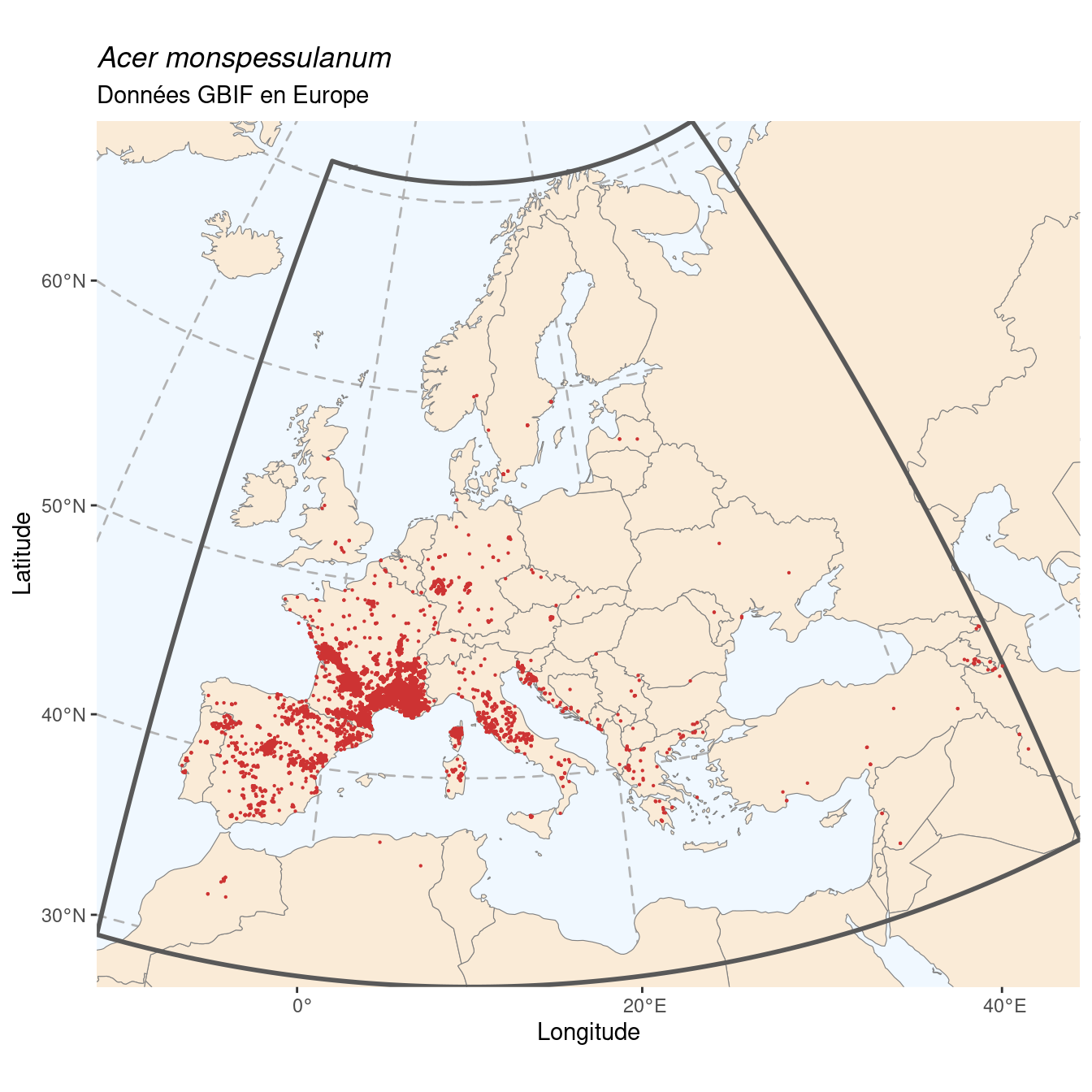
Figure 3.2: Occurrence de Acer monspessulanum en Europe.
3.3.1 Licences
On s’intéresse ici au problème particulier des licences :
CC_BY_4_0
25611
CC_BY_NC_4_0
1750
CC0_1_0
98
https://creativecommons.org/licenses/by-nc/4.0/legalcode
7
https://creativecommons.org/licenses/by/4.0/legalcode
3
https://creativecommons.org/publicdomain/zero/1.0/legalcode
3 
Figure 3.3: Occurrence de Acer monspessulanum en Europe, selon la licence : CC BY-NC en bleu ; CC0 et CC BY en orange.
Les occurrences en CC BY forment l’essentiel du jeu de données. On peut donc supprimer les données en CC BY-NC sans risque.
3.3.2 Sous-échantillonnage
On a légèrement plus de 25 000 localisations ; on procède donc au sous-échantillonnage aléatoire :
Simple feature collection with 25000 features and 50 fields
Attribute-geometry relationship: 50 constant, 0 aggregate, 0 identity
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -9.230237 ymin: 32.5 xmax: 46.900002 ymax: 59.9172
Geodetic CRS: WGS 84
# A tibble: 25,000 × 51
gbifID datasetKey occurrenceID kingdom phylum class order family genus species
<int64> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr>
1 1.95e-314 1579cabf-9d3e-4029-810c-c4a04… a8ad2286-1d… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
2 1.23e-314 fe4baa57-8f75-472b-982a-7711e… 899b216c-aa… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
3 1.72e-314 e5f16d86-e225-4822-97be-a64ce… b6b3b6aa-7f… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
4 5.46e-315 75956ee6-1a2b-4fa3-b3e8-ccda6… http://pifh… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
5 5.46e-315 75956ee6-1a2b-4fa3-b3e8-ccda6… http://flor… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
6 5.46e-315 75956ee6-1a2b-4fa3-b3e8-ccda6… http://flor… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
7 1.47e-314 14d5676a-2c54-4f94-9023-1e8dc… q-101947696… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
8 1.23e-314 3a04668f-4201-47f0-8ec2-69c6d… b6a6d67f-e1… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
9 1.47e-314 14d5676a-2c54-4f94-9023-1e8dc… q-102394947… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
10 1.95e-314 14d5676a-2c54-4f94-9023-1e8dc… q-101072532… Plantae Trach… Magn… Sapi… Sapin… Acer Acer m…
# ℹ 24,990 more rows
# ℹ 41 more variables: infraspecificEpithet <chr>, taxonRank <chr>, scientificName <chr>,
# verbatimScientificName <chr>, verbatimScientificNameAuthorship <chr>, countryCode <chr>,
# locality <chr>, stateProvince <chr>, occurrenceStatus <chr>, individualCount <int>,
# publishingOrgKey <chr>, decimalLatitude <dbl>, decimalLongitude <dbl>,
# coordinateUncertaintyInMeters <dbl>, coordinatePrecision <dbl>, elevation <dbl>,
# elevationAccuracy <dbl>, depth <dbl>, depthAccuracy <dbl>, eventDate <dttm>, day <int>, …3.4 Modélisation de la niche climatique
3.4.1 Préparer les données
Organisation des données d’entrées (occurrences et données environnementales) et des données produites de pseudo-absences :
class : SpatVector
geometry : points
dimensions : 25000, 0 (geometries, attributes)
extent : -9.230237, 46.900002, 32.5, 59.9172 (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat WGS 84 (EPSG:4326)
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= acmo Data Formating -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
! Response variable is considered as only presences... Is it really what you want?
! No data has been set aside for modeling evaluation
!!! Some data are located in the same raster cell.
Please set `filter.raster = TRUE` if you want an automatic filtering.
Checking Pseudo-absence selection arguments...
> random pseudo absences selection
> Pseudo absences are selected in explanatory variables
! Some NAs have been automatically removed from your data
!!! Some data are located in the same raster cell.
Please set `filter.raster = TRUE` if you want an automatic filtering.
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= Done -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= BIOMOD.formated.data -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
dir.name = Output
sp.name = acmo
24991 presences, 0 true absences and 72921 undefined points in dataset
6 explanatory variables
temp_max_august temp_min temp_wet_quart temp_season prec_wet_quart
Min. : 2.82800 Min. :-22.084000 Min. :-11.803333 Min. : 229.4496 Min. : 3.0000
1st Qu.:20.81200 1st Qu.: -8.688000 1st Qu.: 8.984667 1st Qu.: 613.6579 1st Qu.: 181.0000
Median :25.03200 Median : -2.240000 Median : 12.318666 Median : 713.1864 Median : 225.0000
Mean :25.43962 Mean : -3.835936 Mean : 11.996932 Mean : 752.1733 Mean : 227.2461
3rd Qu.:28.32000 3rd Qu.: 1.452000 3rd Qu.: 15.582666 3rd Qu.: 895.6702 3rd Qu.: 274.0000
Max. :46.04800 Max. : 12.124000 Max. : 26.214666 Max. :1394.6377 Max. :1240.0000
prec_season
Min. : 5.945563
1st Qu.: 23.712028
Median : 31.301255
Mean : 35.851783
3rd Qu.: 39.848484
Max. :123.520958
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=On visualise les pseudo-absences :
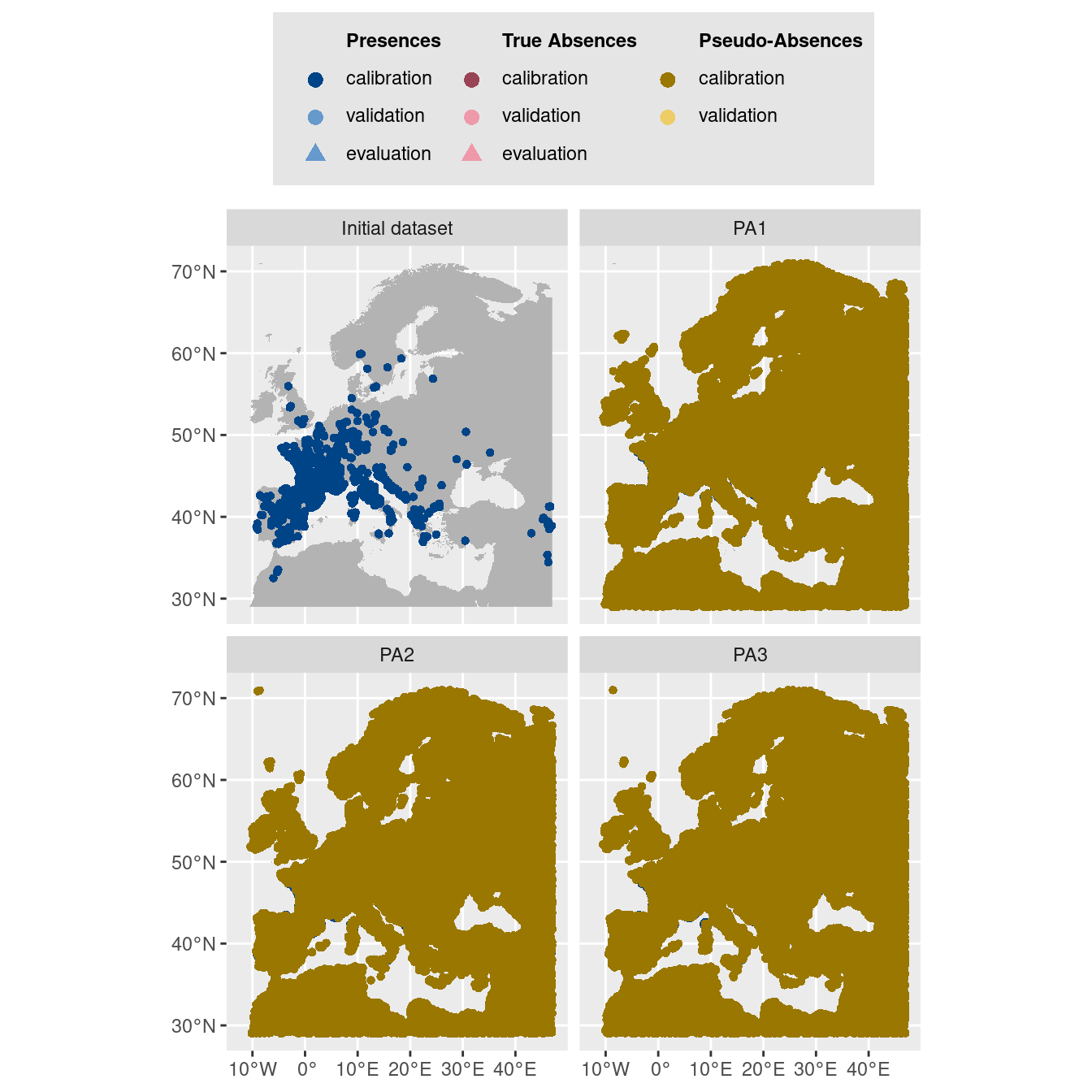
Figure 3.5: Les données d’occurrences (en haut à gauche) et les trois jeux de données aléatoires de pseudo-absences.
$data.vect
class : SpatVector
geometry : points
dimensions : 174964, 2 (geometries, attributes)
extent : -10.52083333, 46.97916667, 29.02083333, 70.97916667 (xmin, xmax, ymin, ymax)
coord. ref. :
names : resp dataset
type : <num> <chr>
values : 10 Initial dataset
10 Initial dataset
10 Initial dataset
$data.label
9 10 11
"**Presences**" "Presences (calibration)" "Presences (validation)"
12 19 20
"Presences (evaluation)" "**True Absences**" "True Absences (calibration)"
21 22 29
"True Absences (validation)" "True Absences (evaluation)" "**Pseudo-Absences**"
30 31 1
"Pseudo-Absences (calibration)" "Pseudo-Absences (validation)" "Background"
$data.plot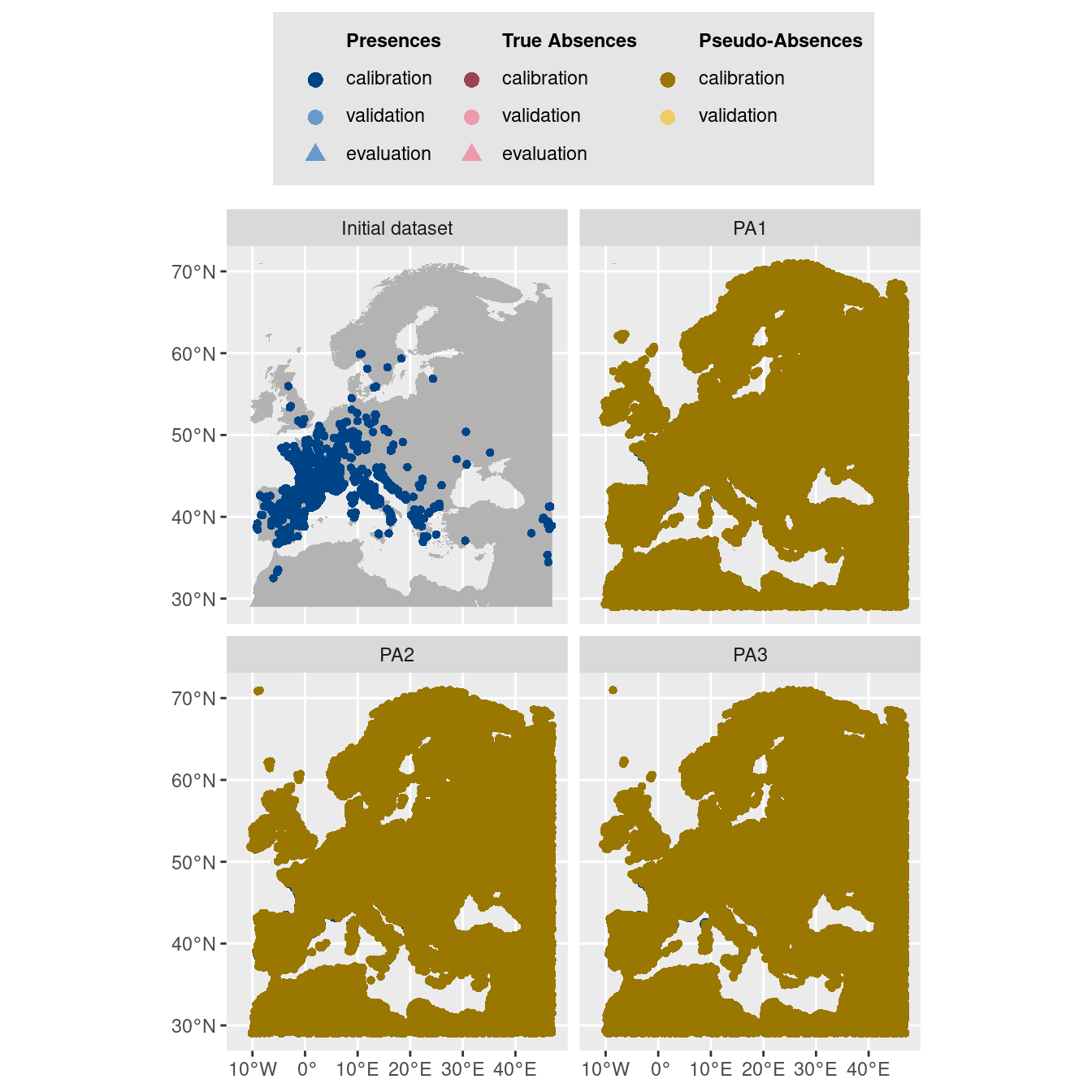
Figure 3.6: Les données d’occurrences (en haut à gauche) et les trois jeux de données aléatoires de pseudo-absences.
3.4.2 Modèles individuels de niche
prendre en compte jeu de données validation
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= Build Single Models -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Checking Models arguments...
! 'MAXENT.Phillips.2' model name is deprecated, please use 'MAXNET' instead.
Creating suitable Workdir...
! Weights where automatically defined for acmo_PA1 to rise a 0.5 prevalence !
! Weights where automatically defined for acmo_PA2 to rise a 0.5 prevalence !
! Weights where automatically defined for acmo_PA3 to rise a 0.5 prevalence !
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= acmo Modeling Summary -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
6 environmental variables ( temp_max_august temp_min temp_wet_quart temp_season prec_wet_quart prec_season )
Number of evaluation repetitions : 1
Models selected : GAM MARS MAXNET GBM ANN RF
Total number of model runs: 18
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
-=-=-=- Run : acmo_PA1
-=-=-=--=-=-=- acmo_PA1_RUN1
-=-=-=- Run : acmo_PA2
-=-=-=--=-=-=- acmo_PA2_RUN1
-=-=-=- Run : acmo_PA3
-=-=-=--=-=-=- acmo_PA3_RUN1
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= Done -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=3.4.2.1 Évaluation de la performance
full.name PA run algo metric.eval cutoff sensitivity specificity calibration
1 acmo_PA1_RUN1_GAM PA1 RUN1 GAM TSS 747.0 97.349 64.130 0.615
2 acmo_PA1_RUN1_GAM PA1 RUN1 GAM ROC 750.5 97.334 64.185 0.715
3 acmo_PA1_RUN1_MARS PA1 RUN1 MARS TSS 585.0 93.768 92.140 0.859
4 acmo_PA1_RUN1_MARS PA1 RUN1 MARS ROC 591.5 93.733 92.255 0.978
5 acmo_PA1_RUN1_MAXNET PA1 RUN1 MAXNET TSS 331.0 96.264 91.220 0.875
6 acmo_PA1_RUN1_MAXNET PA1 RUN1 MAXNET ROC 331.5 96.259 91.275 0.978
validation evaluation
1 0.610 NA
2 0.711 NA
3 0.860 NA
4 0.977 NA
5 0.872 NA
6 0.976 NA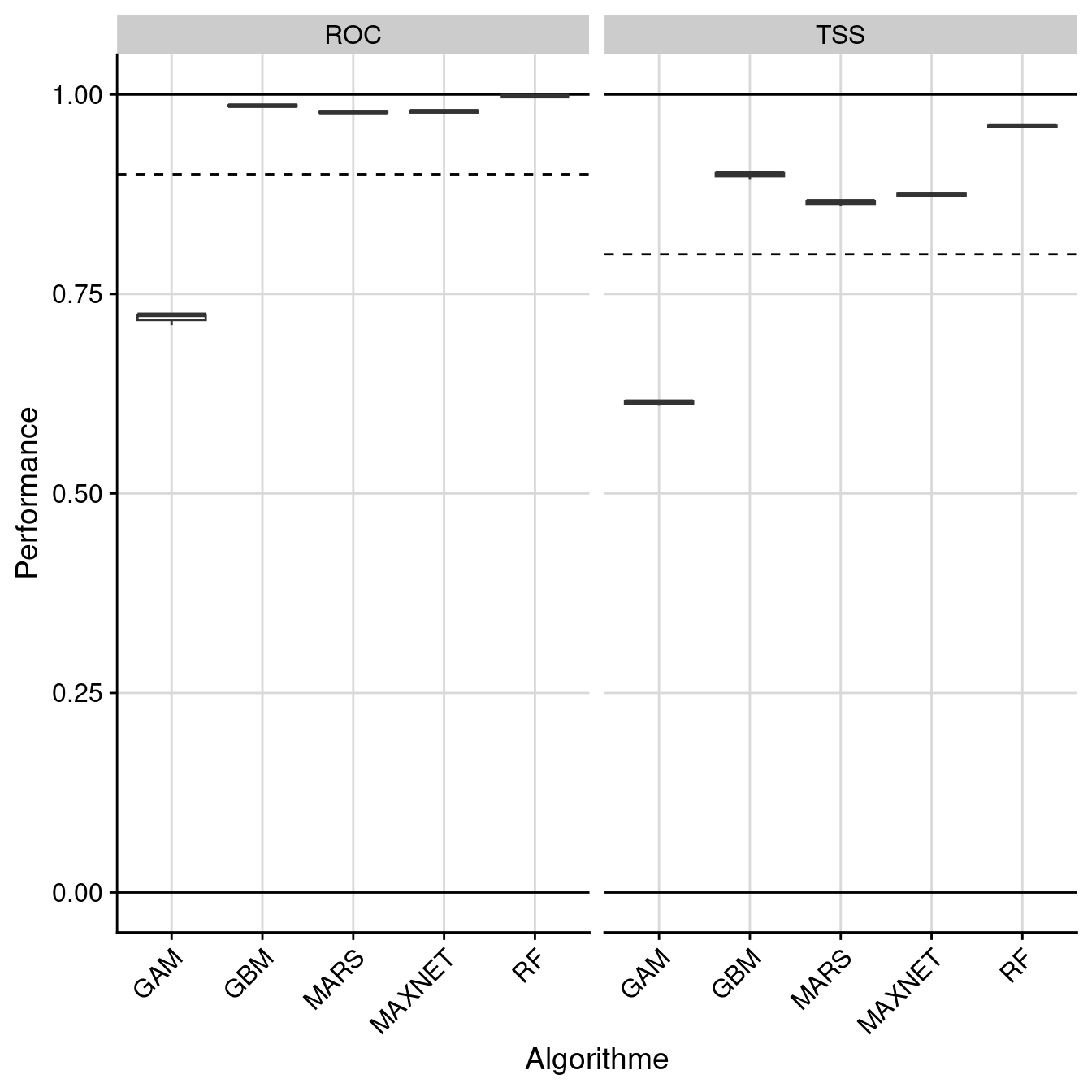
Figure 3.7: Évaluation de la performance des modèles individuels : True Skill Statistic & aire sous la courbe de ROC.
Les GAMs, et une partie des ANNs ont une performance médiocre, et seront automatiquement exclus pour les modèles d’ensemble.
3.4.2.2 Importance des variables environnementales
L’importance de chaque variable est estimée par randomisation de la variable
d’intérêt (moyenne/variance sur tous les algorithmes). On utilise la fonction
get_variables_importance() pour récupérer l’importance des variables, que l’on
peut visualiser par algorithme ou par variable :
full.name PA run algo expl.var rand var.imp
1 acmo_PA1_RUN1_GAM PA1 RUN1 GAM temp_max_august 1 0.531386
2 acmo_PA1_RUN1_GAM PA1 RUN1 GAM temp_min 1 0.111026
3 acmo_PA1_RUN1_GAM PA1 RUN1 GAM temp_wet_quart 1 0.037930
4 acmo_PA1_RUN1_GAM PA1 RUN1 GAM temp_season 1 0.607463
5 acmo_PA1_RUN1_GAM PA1 RUN1 GAM prec_wet_quart 1 0.018929
6 acmo_PA1_RUN1_GAM PA1 RUN1 GAM prec_season 1 0.029839
Figure 3.8: Pourcentage de variance expliquée pour chaque variable, décomposé par algorithme.
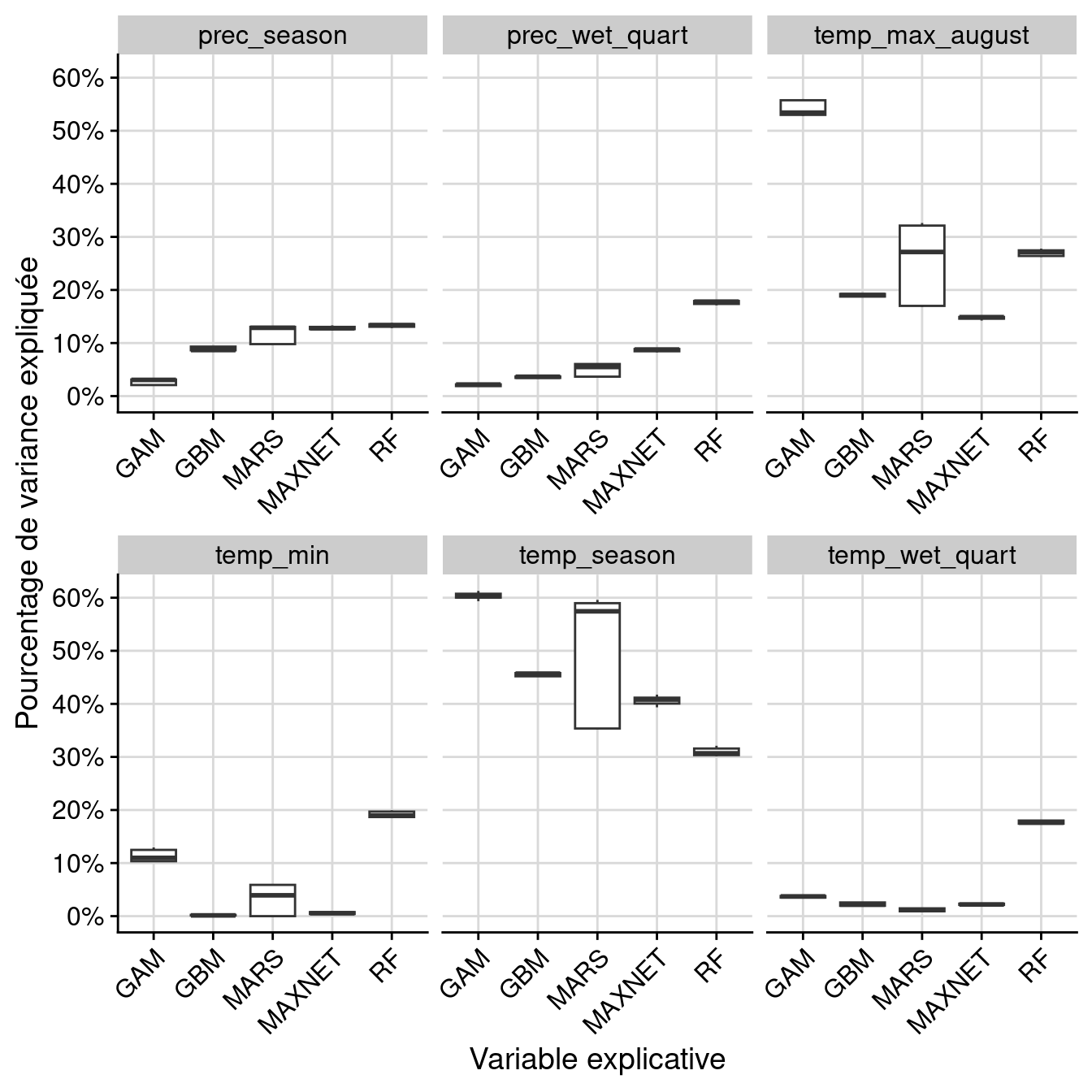
Figure 3.9: Pourcentage de variance expliquée pour chaque variable, décomposé par variable.
3.4.2.3 Courbes de réponse
Finalement, le modèle permet d’établir des courbes de réponse, c’est-à-dire la
variation de la probabilité d’occurrence selon chaque variable
environnementale. On utilise pour cela la fonction bm_PlotResponseCurves() qui
permet d’extraire ces valeurs et de les afficher :
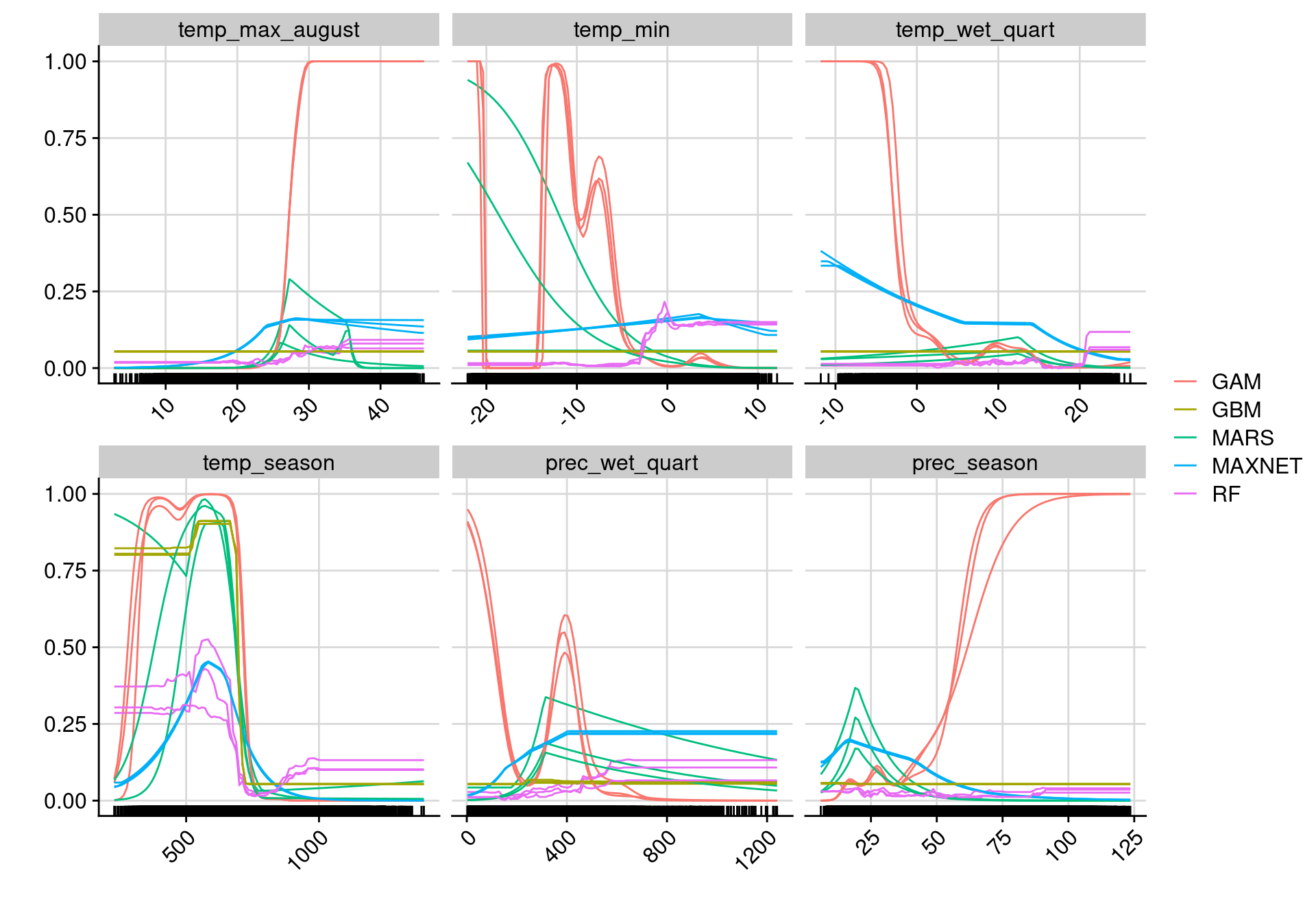
Figure 3.10: Courbes de réponse de chaque variable climatique selon l’algorithme (en couleurs).
3.4.3 Modèles d’ensemble de niche
Seulement modèles avec TSS > 0.8
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= BIOMOD.ensemble.models.out -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
sp.name : acmo
expl.var.names : temp_max_august temp_min temp_wet_quart temp_season prec_wet_quart prec_season
models computed:
acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo, acmo_EMwmeanByTSS_mergedData_mergedRun_mergedAlgo
models failed: none
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=→ prend les modèles individuels en entrée → on décide sur quel critère les modèles sont gardés
même idée que l’interférence multi-modèles, mais basé sur métrique de performance (e.g. TSS > 0.8 et AUC/ROC > 0.9)
→ on peut calculer moyenne ou médiane → retourne des coefficients de variation → retourne des probabilités pondérées par la métrique choisie
→ grouping level stratifié jusqu’à “all”
3.4.3.1 Évaluation de la qualité
get_evaluations() pour récupérer les stats d’intérêt
full.name merged.by.PA merged.by.run merged.by.algo
1 acmo_EMwmeanByTSS_mergedData_mergedRun_mergedAlgo mergedData mergedRun mergedAlgo
2 acmo_EMwmeanByTSS_mergedData_mergedRun_mergedAlgo mergedData mergedRun mergedAlgo
filtered.by algo metric.eval cutoff sensitivity specificity calibration validation evaluation
1 TSS EMwmean TSS 541.0 97.003 96.349 0.934 NA NA
2 TSS EMwmean ROC 542.5 96.995 96.392 0.996 NA NA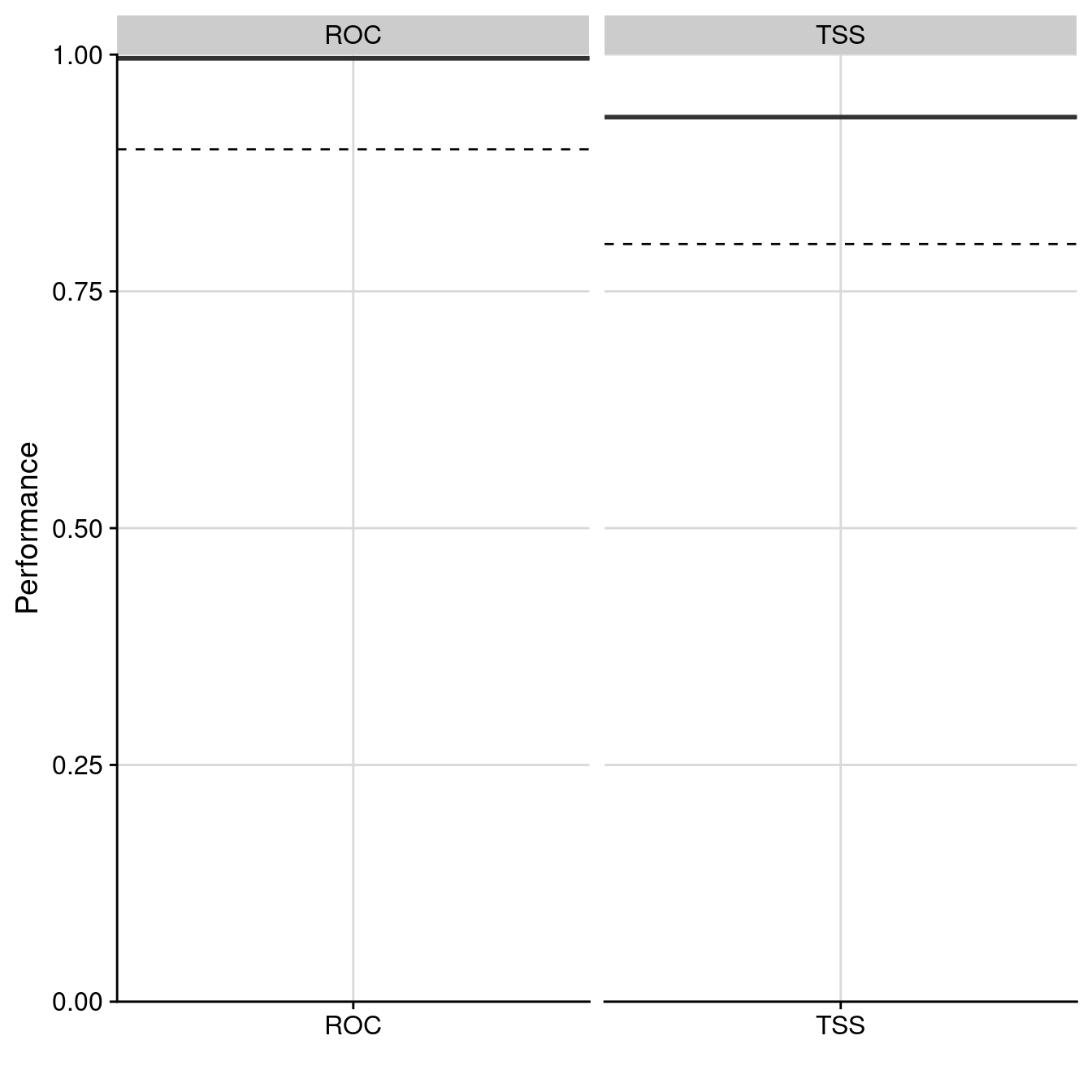
Figure 3.11: Évaluation de la qualité du modèle d’ensemble : Aire sous la courbe de ROC & True Skill Statistic.
full.name merged.by.PA merged.by.run merged.by.algo filtered.by
1 acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo mergedData mergedRun mergedAlgo TSS
2 acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo mergedData mergedRun mergedAlgo TSS
3 acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo mergedData mergedRun mergedAlgo TSS
4 acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo mergedData mergedRun mergedAlgo TSS
5 acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo mergedData mergedRun mergedAlgo TSS
6 acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo mergedData mergedRun mergedAlgo TSS
algo expl.var rand var.imp
1 EMcv temp_max_august 1 0.190449
2 EMcv temp_min 1 0.119873
3 EMcv temp_wet_quart 1 0.072965
4 EMcv temp_season 1 0.383299
5 EMcv prec_wet_quart 1 0.113879
6 EMcv prec_season 1 0.111513Par variable :
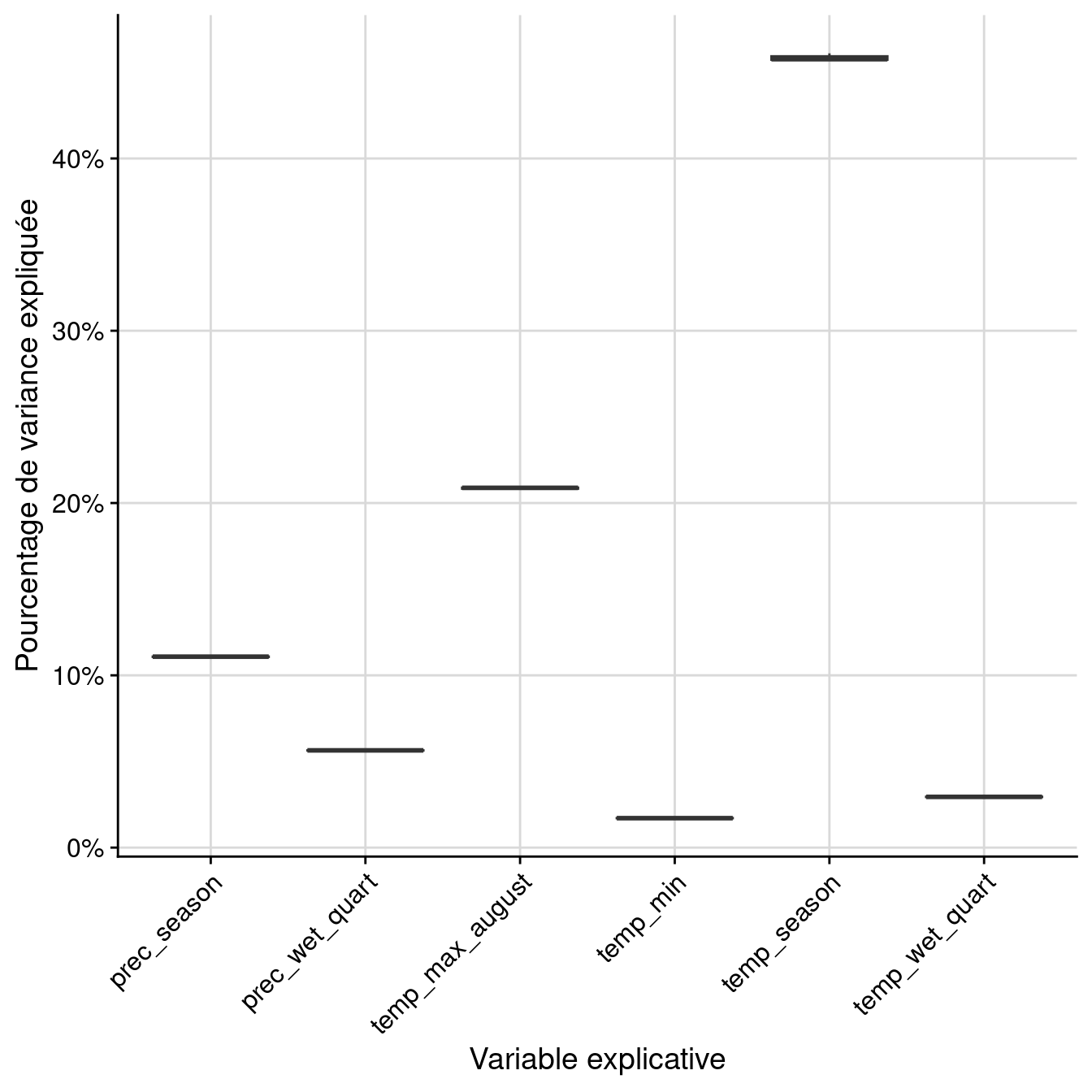
Figure 3.12: Pourcentage de variance expliquée par variable dans le modèle d’ensemble.
bm_PlotResponseCurves() pour forme de la réponse sur chaque variable
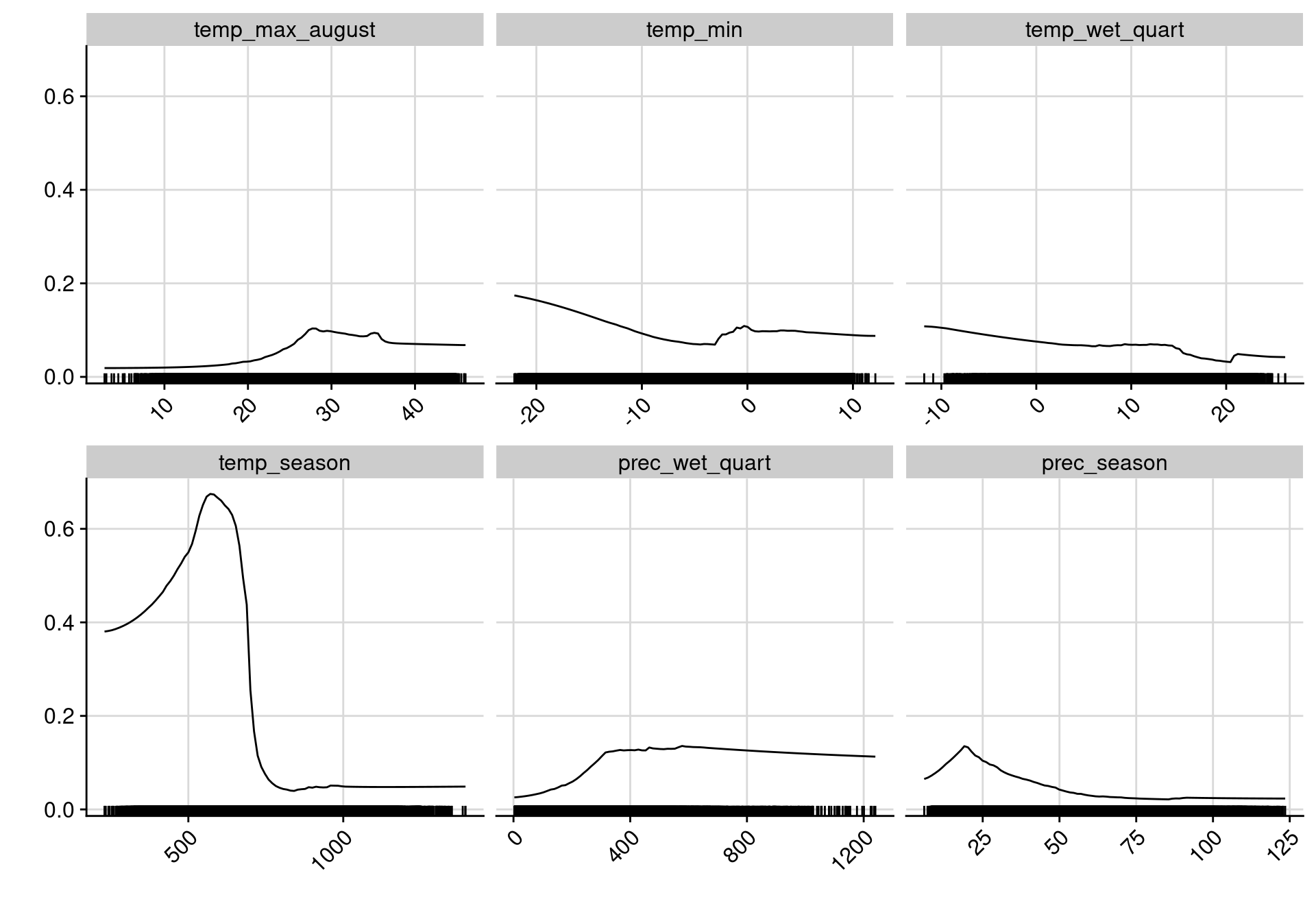
Figure 3.13: Courbes de réponse de chaque variable climatique dans le modèle d’ensemble.
3.5 Projections
3.5.1 Distribution potentielle contemporaine
Contemporaine : Cartographie des observations sur couches climatiques Extraction des conditions climatiques favorables
BIOMOD_Projection() un seul modèle
BIOMOD_EnsembleForecasting() modèle d’ensemble
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= BIOMOD.projection.out -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Projection directory : Output/acmo/current
sp.name : acmo
expl.var.names : temp_max_august temp_min temp_wet_quart temp_season prec_wet_quart prec_season
modeling.id : AllModels ( Output/acmo/acmo.AllModels.models.out )
models.projected :
acmo_PA1_RUN1_GAM, acmo_PA1_RUN1_MARS, acmo_PA1_RUN1_MAXNET, acmo_PA1_RUN1_GBM, acmo_PA1_RUN1_RF, acmo_PA2_RUN1_GAM, acmo_PA2_RUN1_MARS, acmo_PA2_RUN1_MAXNET, acmo_PA2_RUN1_GBM, acmo_PA2_RUN1_RF, acmo_PA3_RUN1_GAM, acmo_PA3_RUN1_MARS, acmo_PA3_RUN1_MAXNET, acmo_PA3_RUN1_GBM, acmo_PA3_RUN1_RF
available binary projection : TSS, ROC
available filtered projection : TSS, ROC
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=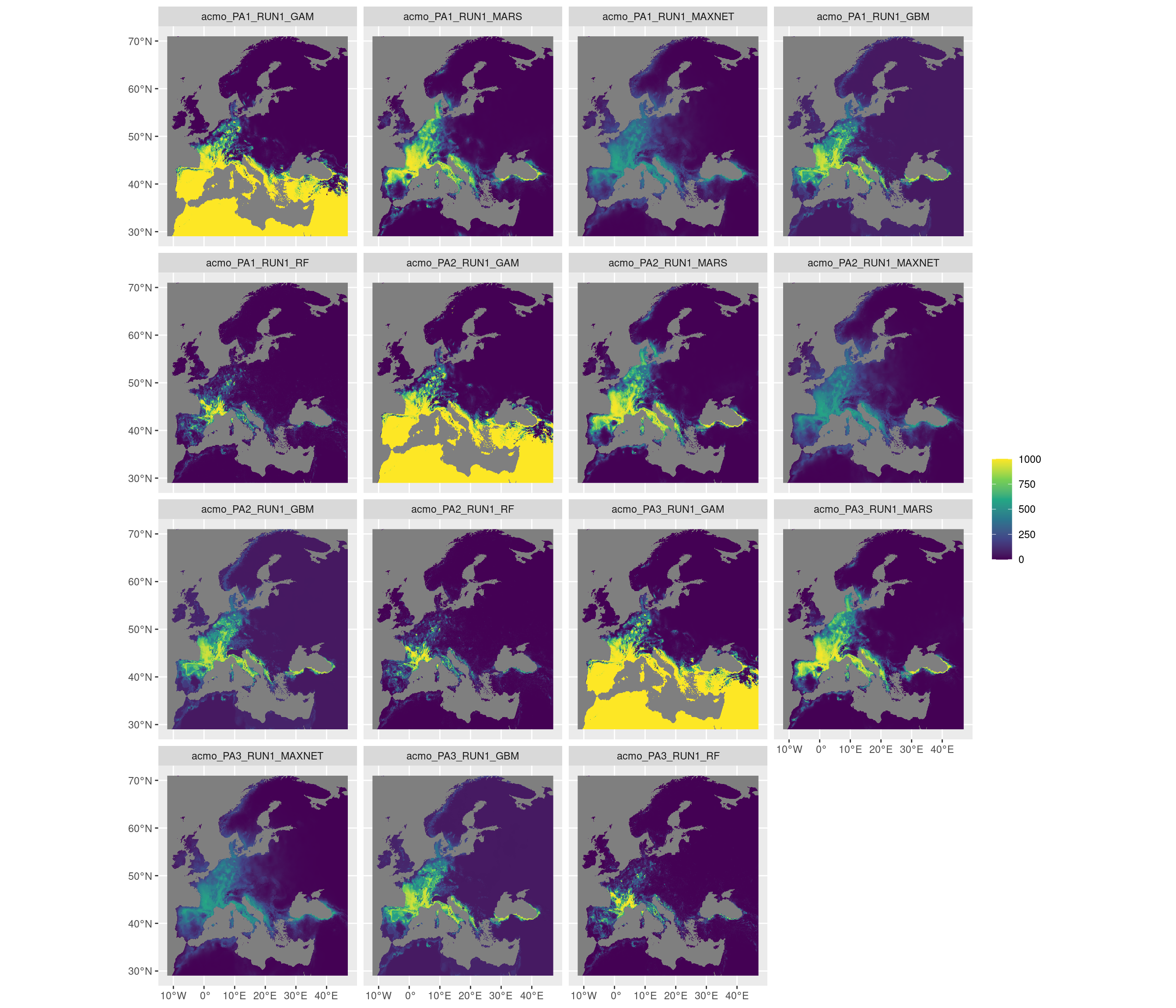
Figure 3.14: Projection de la distribution potentielle contemporaine sur l’Europe, selon les 6 algorithmes et les 3 runs.
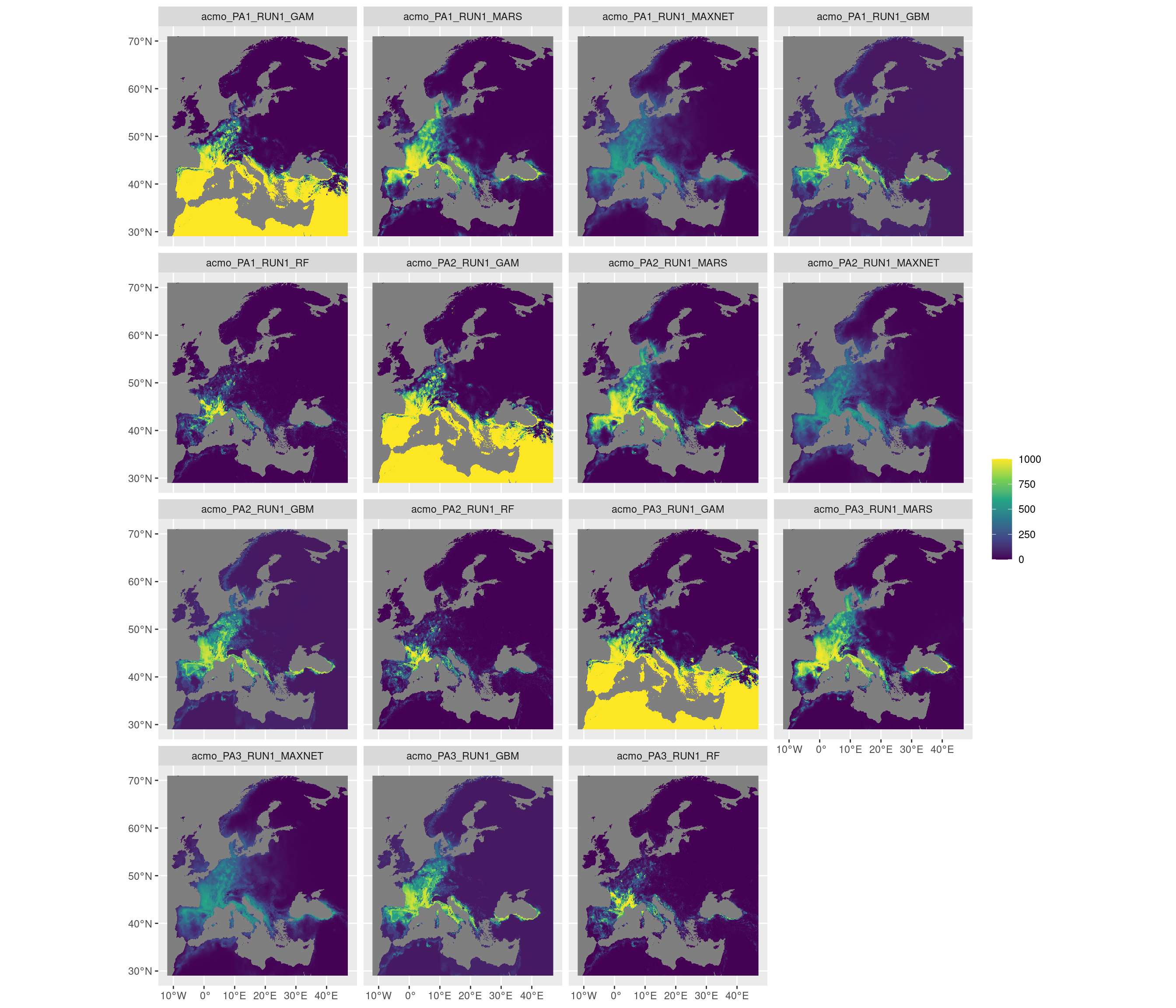
Figure 3.15: Projection de la distribution potentielle contemporaine sur l’Europe, selon les 6 algorithmes et les 3 runs.
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= BIOMOD.projection.out -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Projection directory : Output/acmo/current
sp.name : acmo
expl.var.names : temp_max_august temp_min temp_wet_quart temp_season prec_wet_quart prec_season
modeling.id : AllModels ( Output/acmo/acmo.AllModels.ensemble.models.out )
models.projected :
acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo, acmo_EMwmeanByTSS_mergedData_mergedRun_mergedAlgo
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=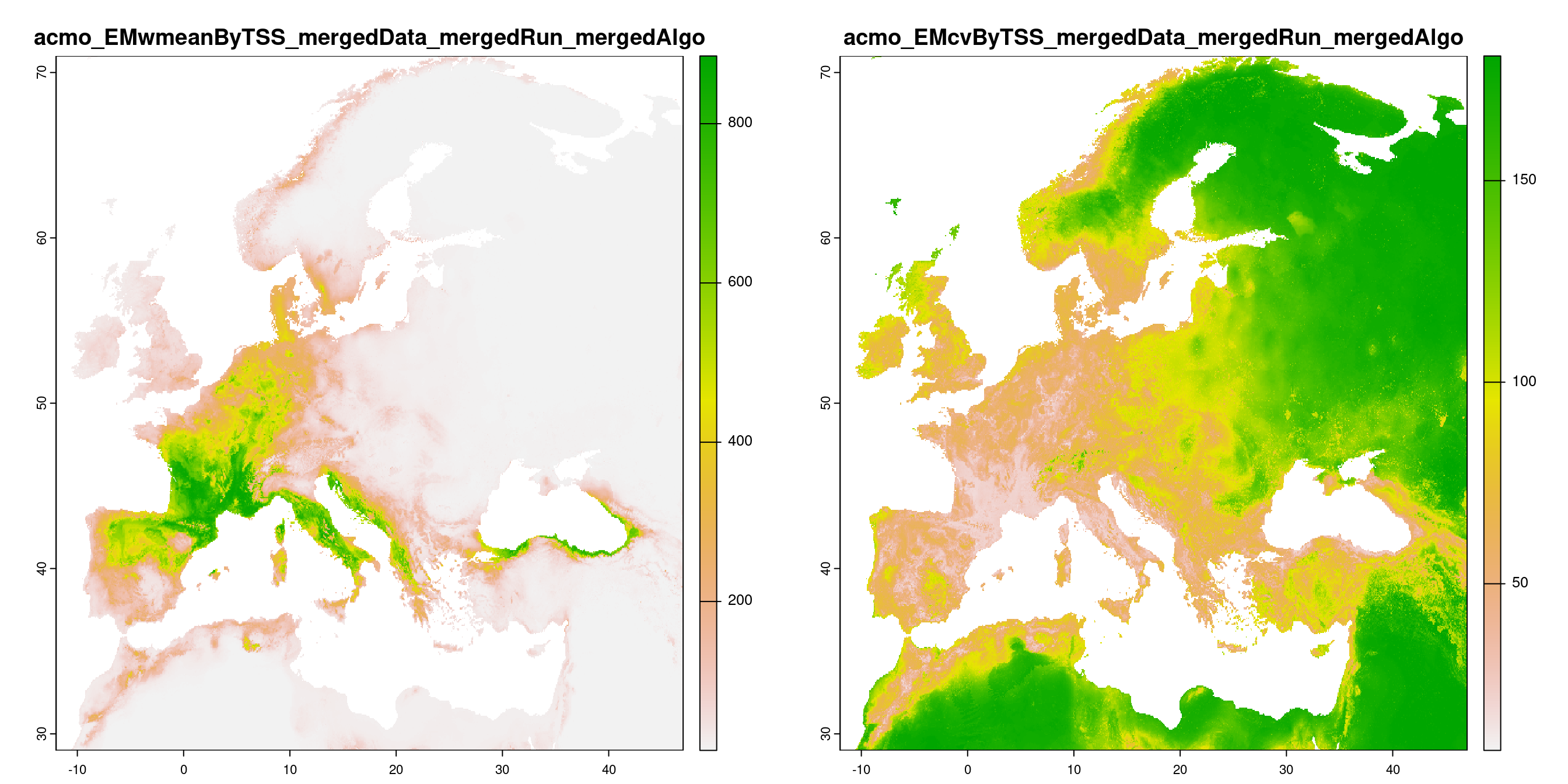
Figure 3.16: A) Projection de la distribution potentielle contemporaine (modèle d’ensemble) ; B) Incertitude associée à la projection.
3.5.2 Interpolation à l’échelle de la métropole
- → conditions climatiques favorables à fine échelle
On projette la niche climatique sur ce raster à fine échelle.
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= BIOMOD.projection.out -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Projection directory : Output/acmo/cont_gre
sp.name : acmo
expl.var.names : temp_max_august temp_min temp_wet_quart temp_season prec_wet_quart prec_season
modeling.id : AllModels ( Output/acmo/acmo.AllModels.models.out )
models.projected :
acmo_PA1_RUN1_GAM, acmo_PA1_RUN1_MARS, acmo_PA1_RUN1_MAXNET, acmo_PA1_RUN1_GBM, acmo_PA1_RUN1_RF, acmo_PA2_RUN1_GAM, acmo_PA2_RUN1_MARS, acmo_PA2_RUN1_MAXNET, acmo_PA2_RUN1_GBM, acmo_PA2_RUN1_RF, acmo_PA3_RUN1_GAM, acmo_PA3_RUN1_MARS, acmo_PA3_RUN1_MAXNET, acmo_PA3_RUN1_GBM, acmo_PA3_RUN1_RF
available binary projection : TSS, ROC
available filtered projection : TSS, ROC
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=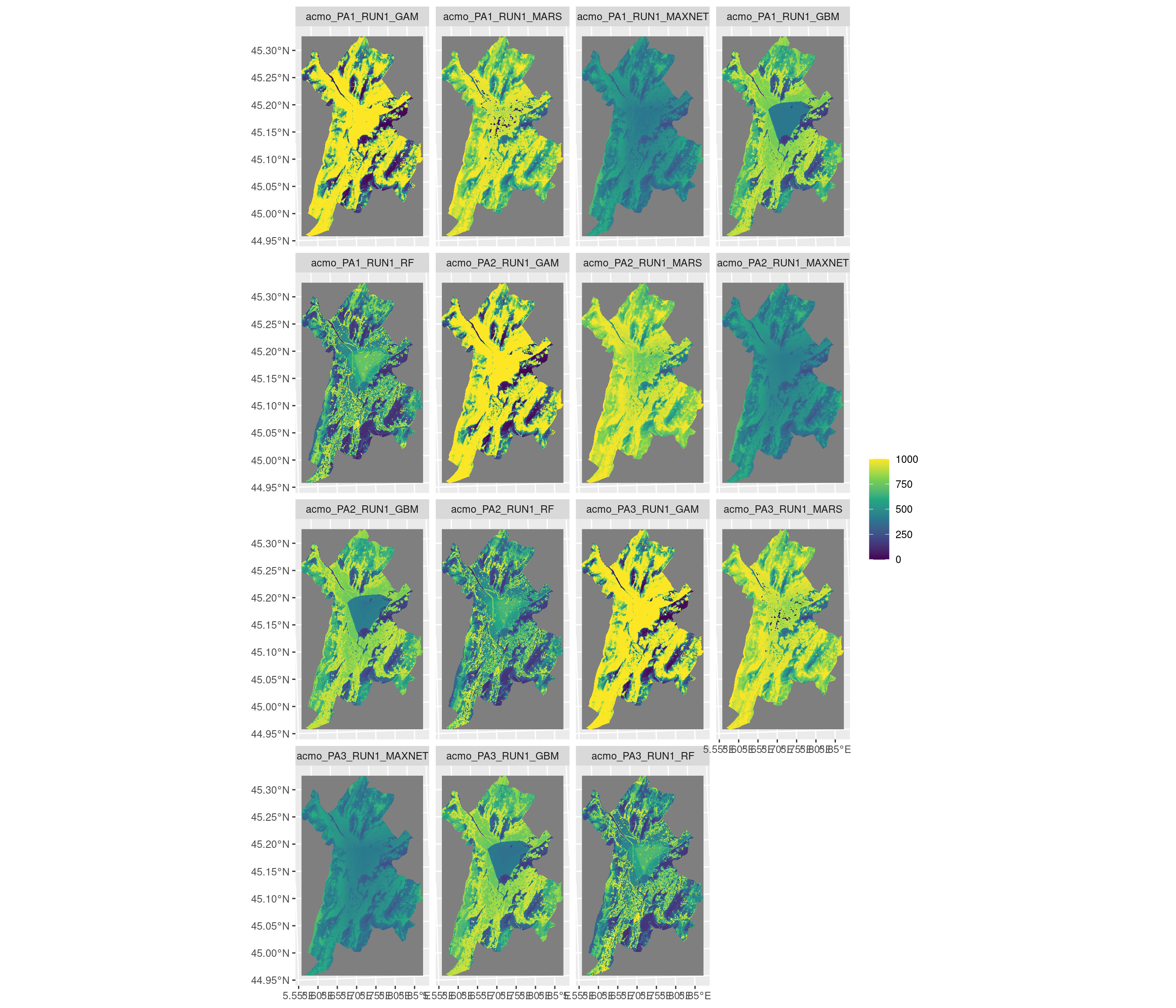
Figure 3.17: Projection de la distribution potentielle contemporaine sur la métropole de Grenoble, selon les 6 algorithmes et les 3 runs.
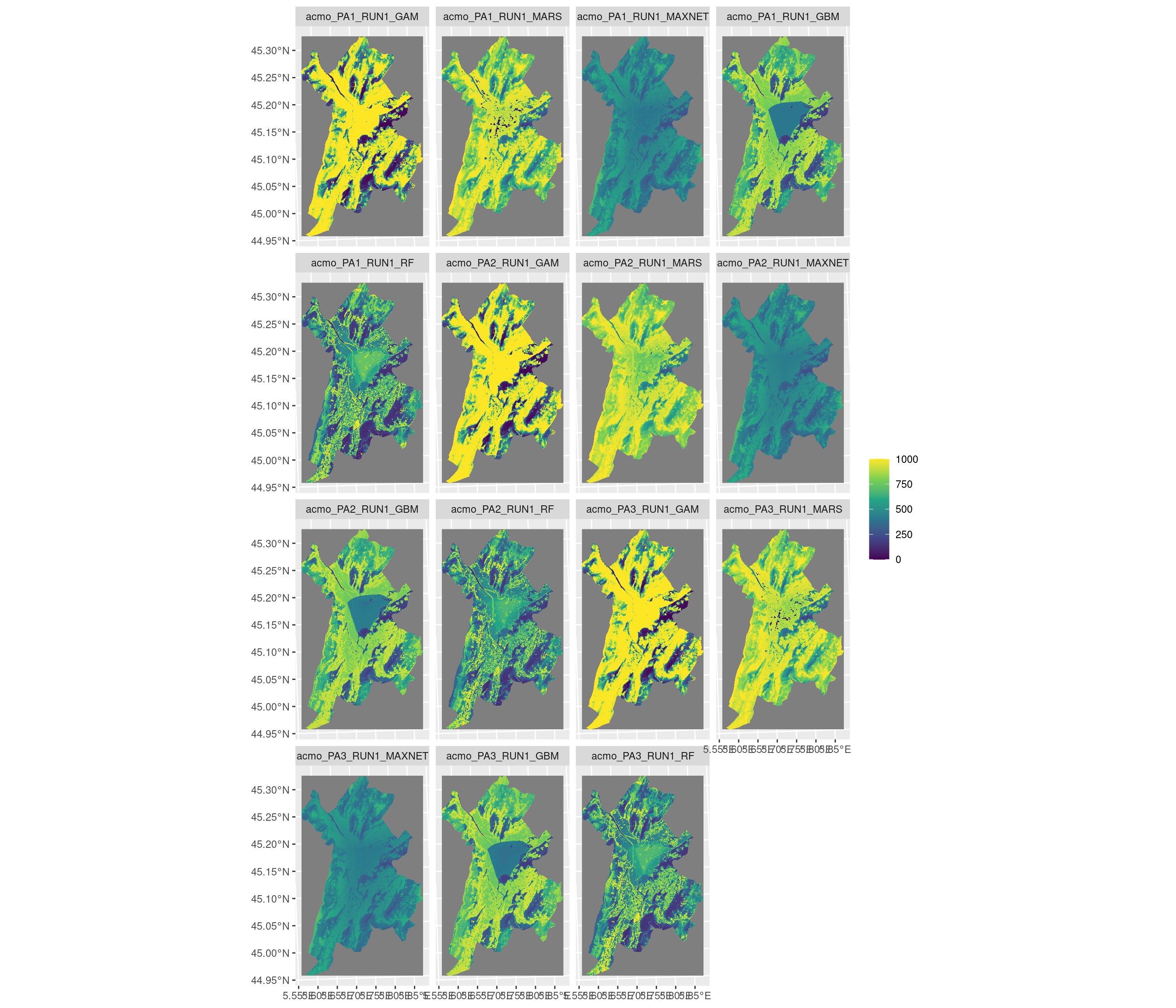
Figure 3.18: Projection de la distribution potentielle contemporaine sur la métropole de Grenoble, selon les 6 algorithmes et les 3 runs.
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-= BIOMOD.projection.out -=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Projection directory : Output/acmo/cont_gre
sp.name : acmo
expl.var.names : temp_max_august temp_min temp_wet_quart temp_season prec_wet_quart prec_season
modeling.id : AllModels ( Output/acmo/acmo.AllModels.ensemble.models.out )
models.projected :
acmo_EMcvByTSS_mergedData_mergedRun_mergedAlgo, acmo_EMwmeanByTSS_mergedData_mergedRun_mergedAlgo
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=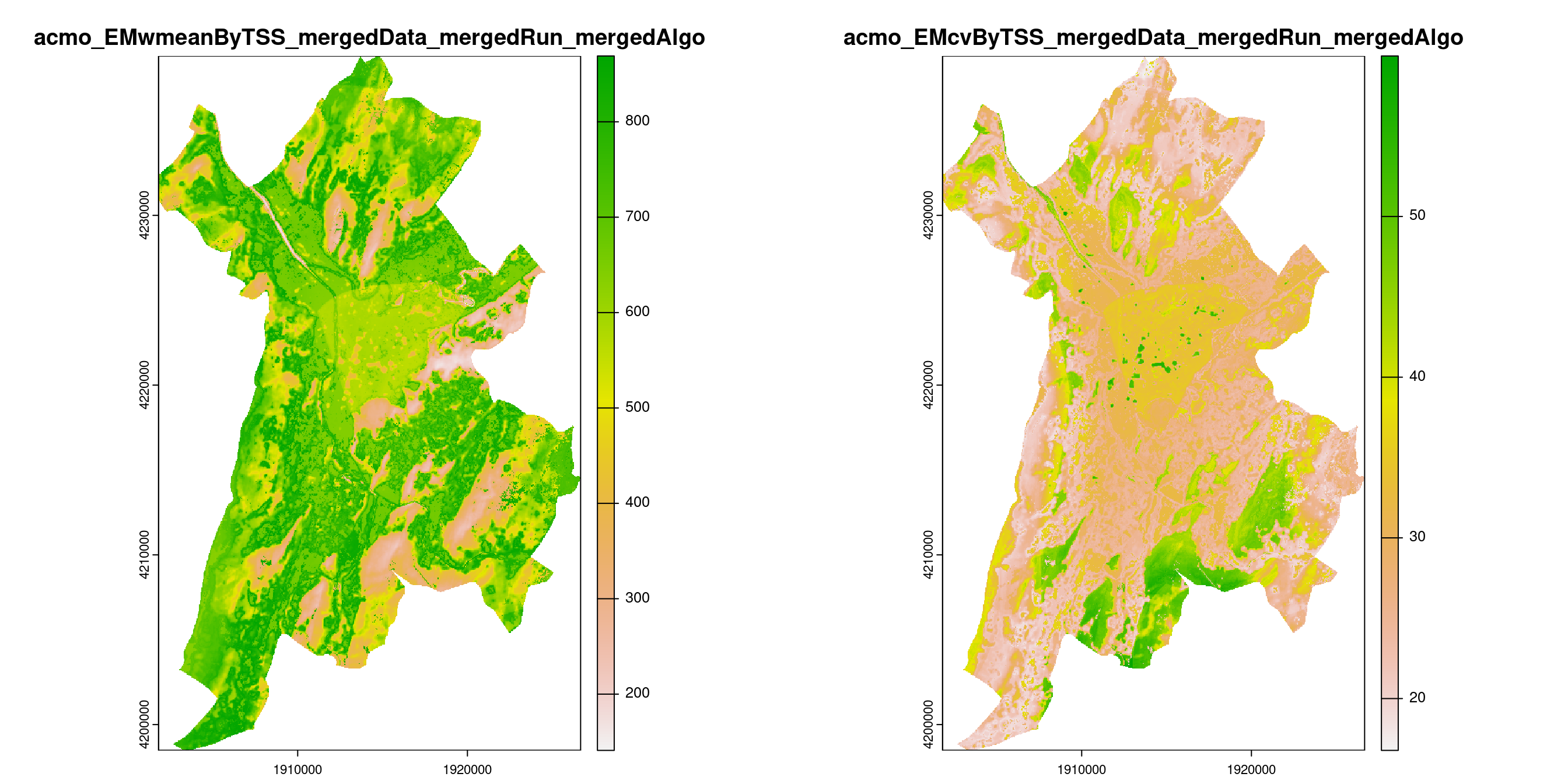
Figure 3.19: A) Projection de la distribution potentielle contemporaine (modèle d’ensemble) sur la métropole de Grenoble ; B) Incertitude associée à la projection.
3.5.3 Validation avec une référence française (IFN)
extraction des pixels par polygone (écorégion) et moyenne arithmétique pour chacun :
acmo_density acmo_current_proj
1 0 100.3276892
2 0 202.2655502
3 0 269.3477322
4 0 209.1653117
5 0 485.8800539
6 0 562.2042553IFN pour ACMO, densité + Carte de projection actuelle France


Figure 3.20: A) Carte de densité selon l’IFN ; B) Probabilité d’occurrence selon le modèle d’ensemble.
corrélation non paramétrique de Spearman (par les rangs) :
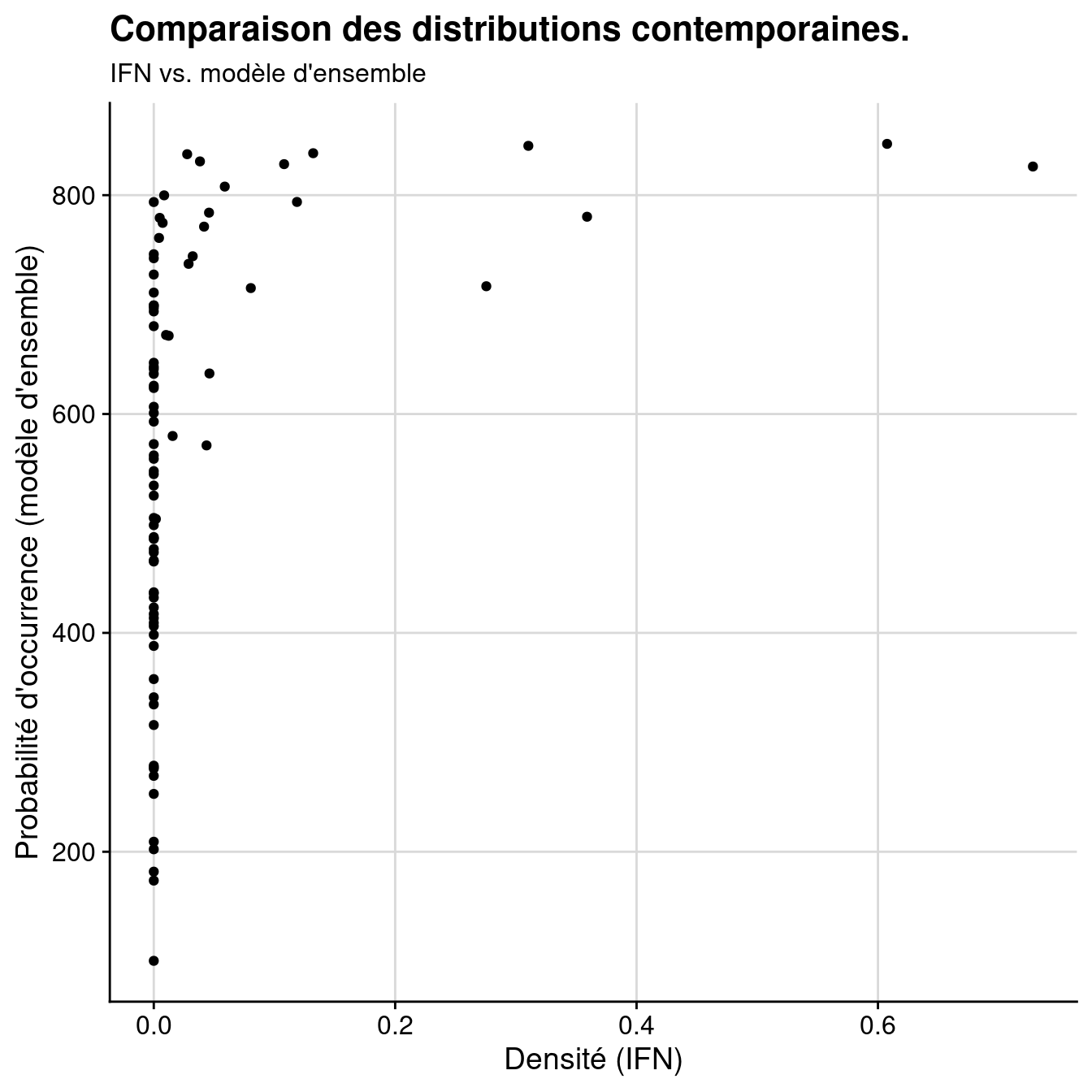
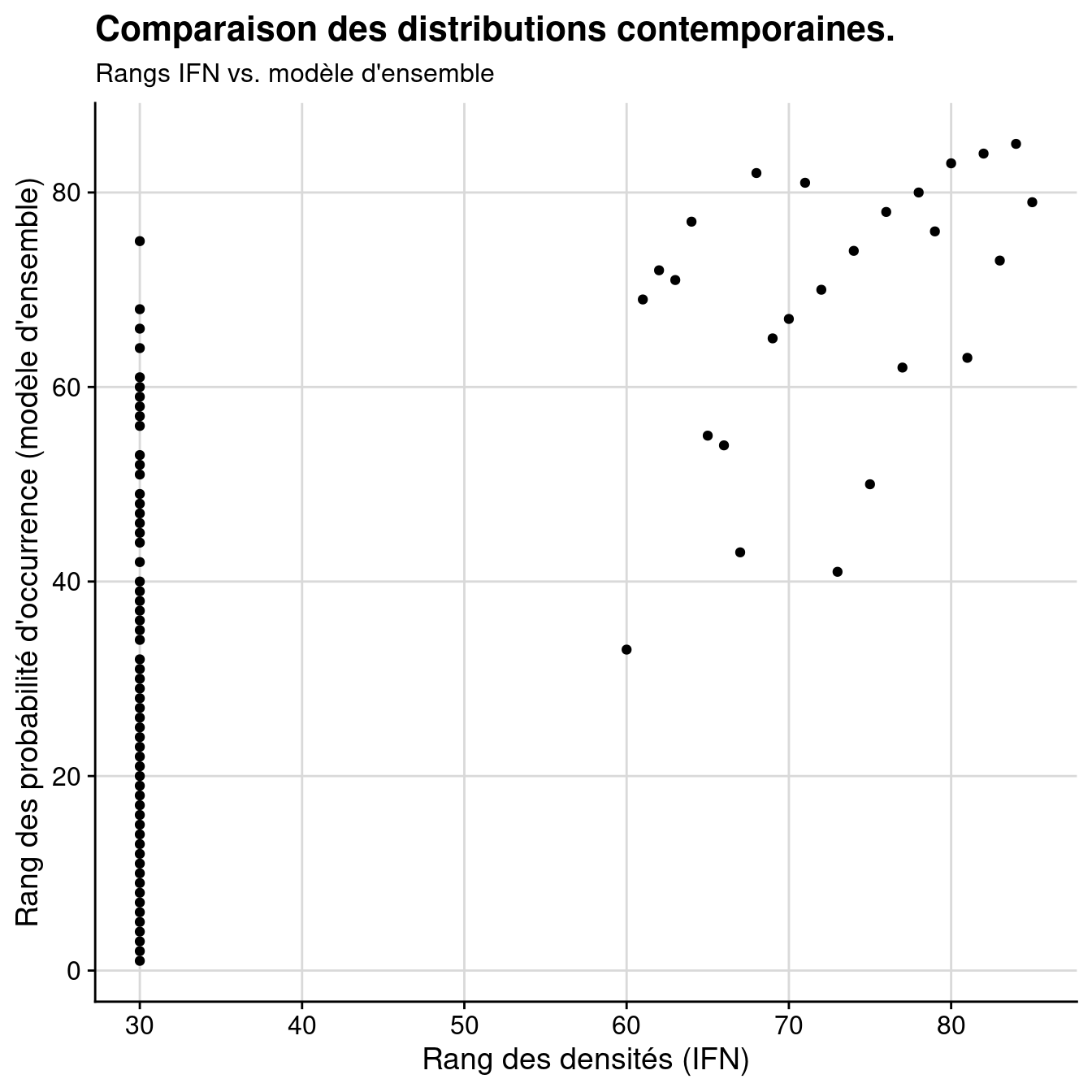
Figure 3.21: Comparaison des distributions contemporaines données par l’IFN vs. modèle d’ensemble : A) Données brutes ; B) Rangs.
[1] 0.68988632573.5.4 Distributions potentielles futures
Future : Projection à l’échelle de l’Europe jusqu’à l’horizon 2100
Toutes les fenêtres temporelles × scénarios pour le GCM « IPSL-CM6A-LR »
- SSP1-2.6
On peut évaluer directement la sortie du modèle d’ensemble.
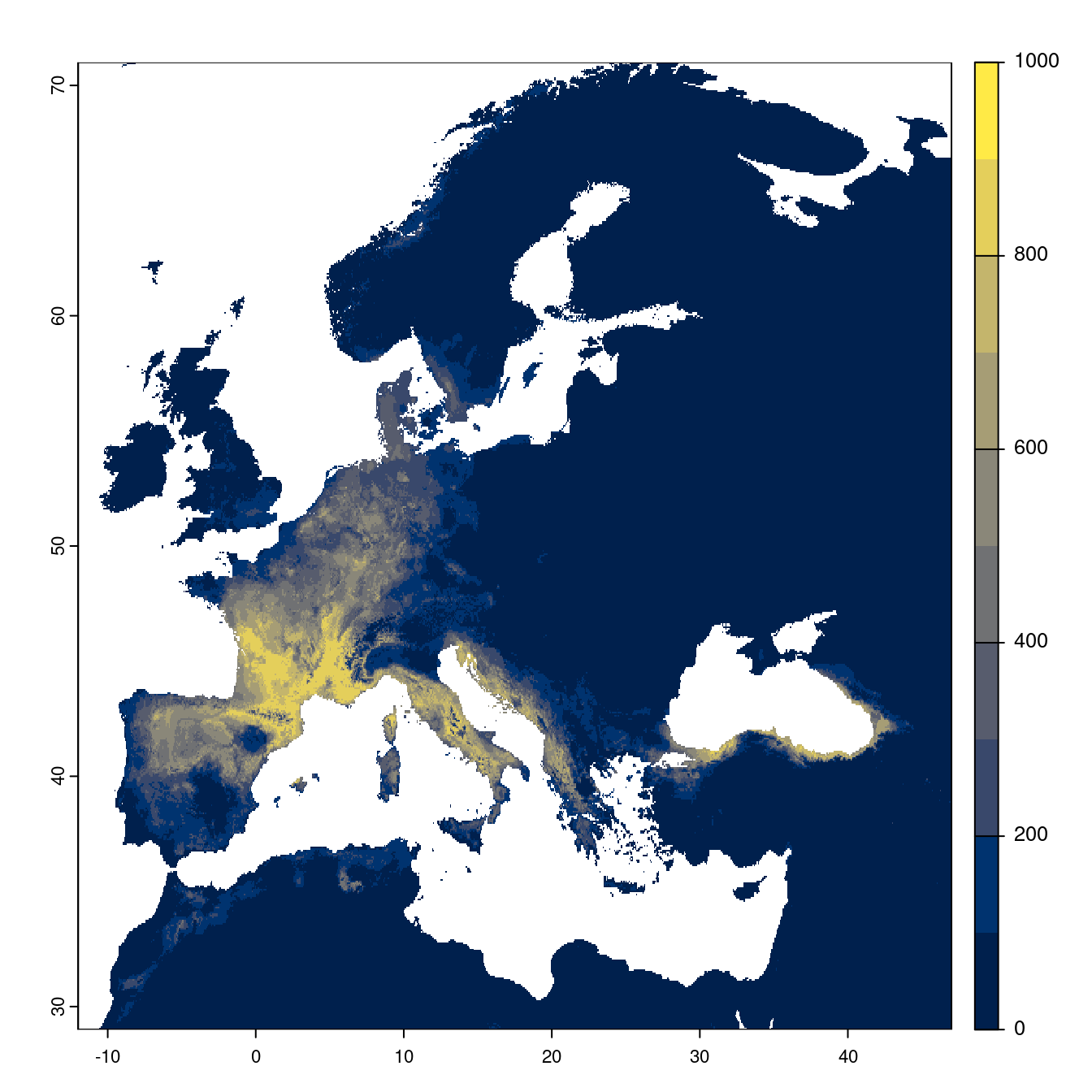
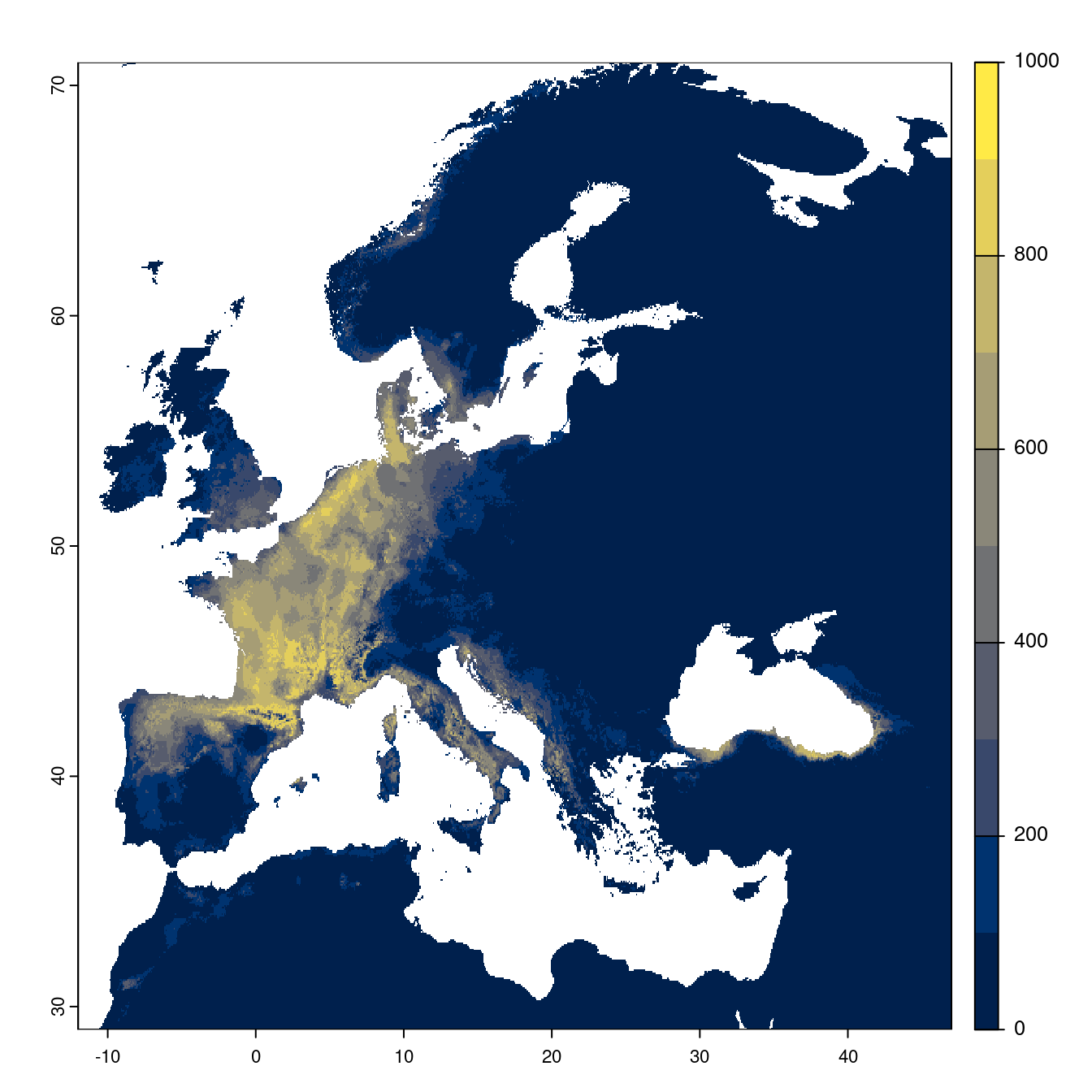
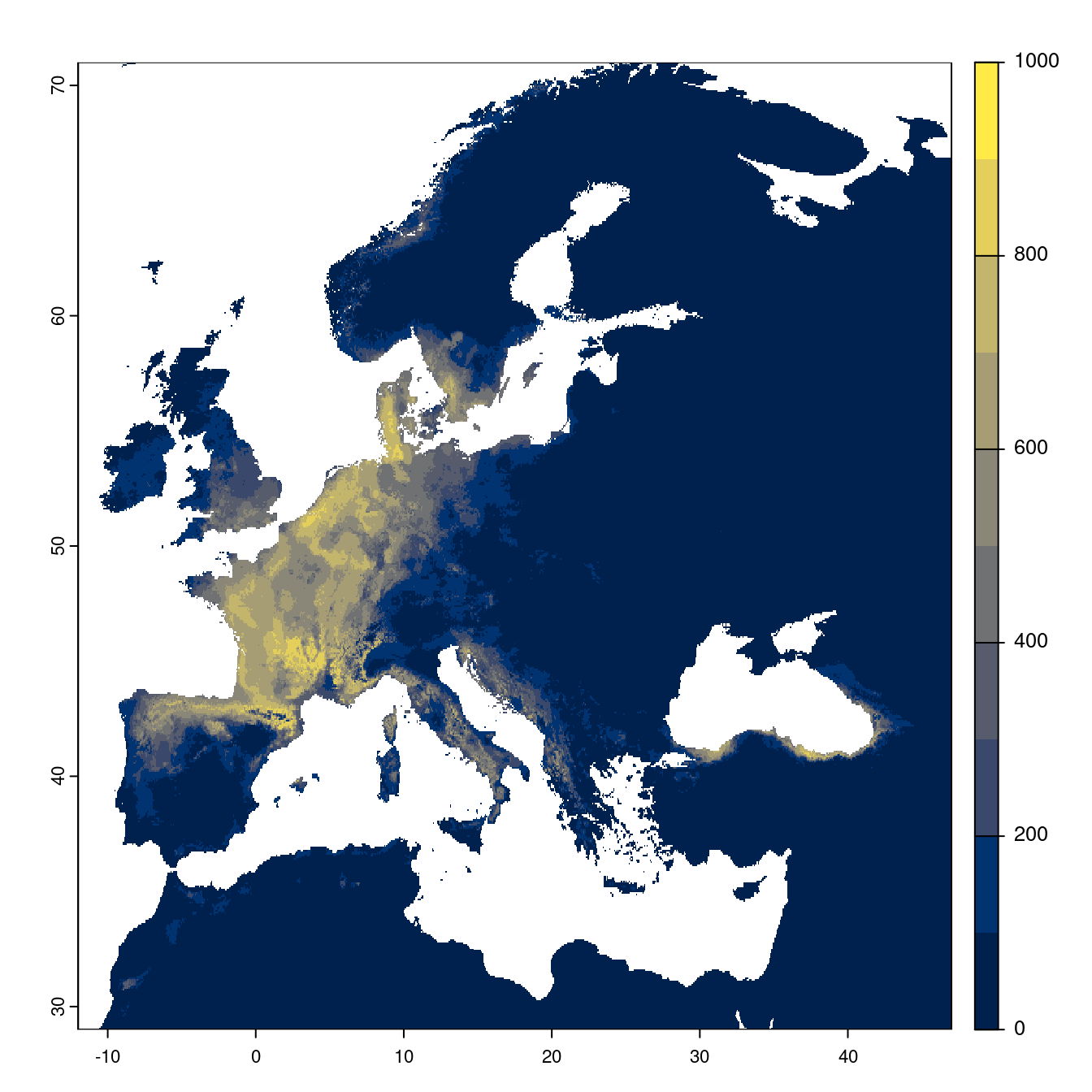
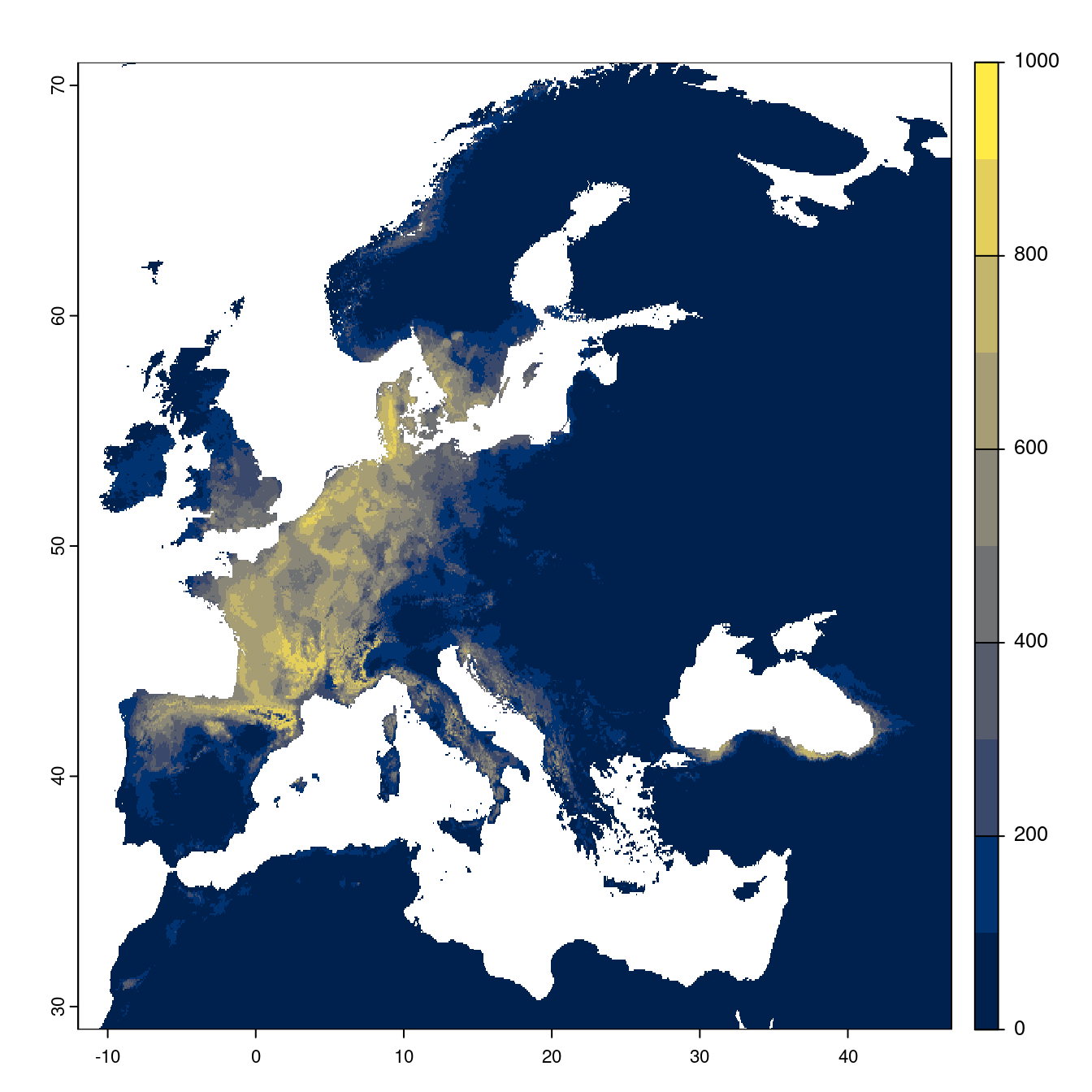
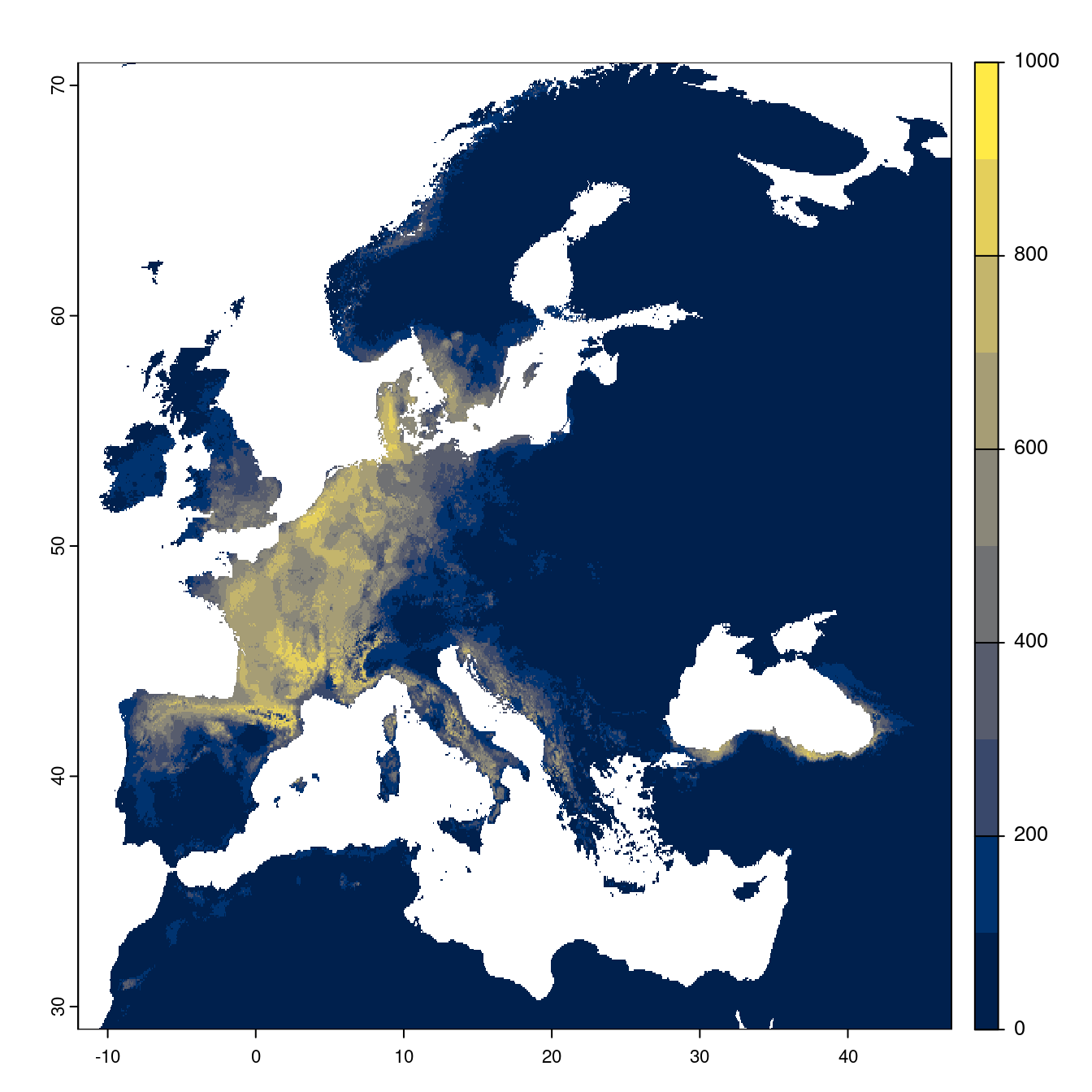
Figure 3.22: Projection des distributions potentielles futures jusqu’à l’horizon 2100 sous le scénario SSP1-2.6 (modèle d’ensemble).
On obtient pour la métrique TSS une carte unique de moyenne pondérée sur les algorithmes et sur les jeux de pseudo-absences.
- SSP2-4.5
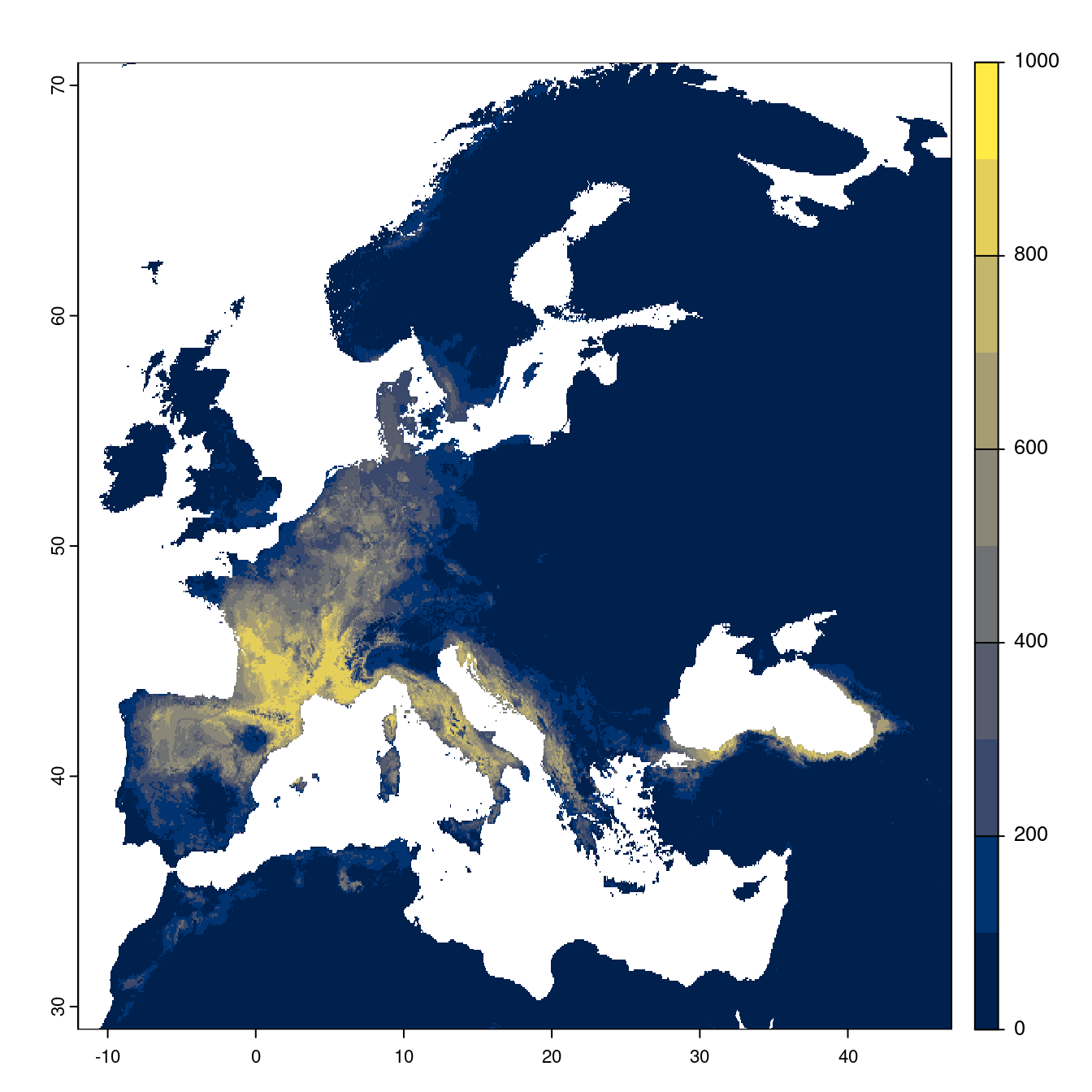
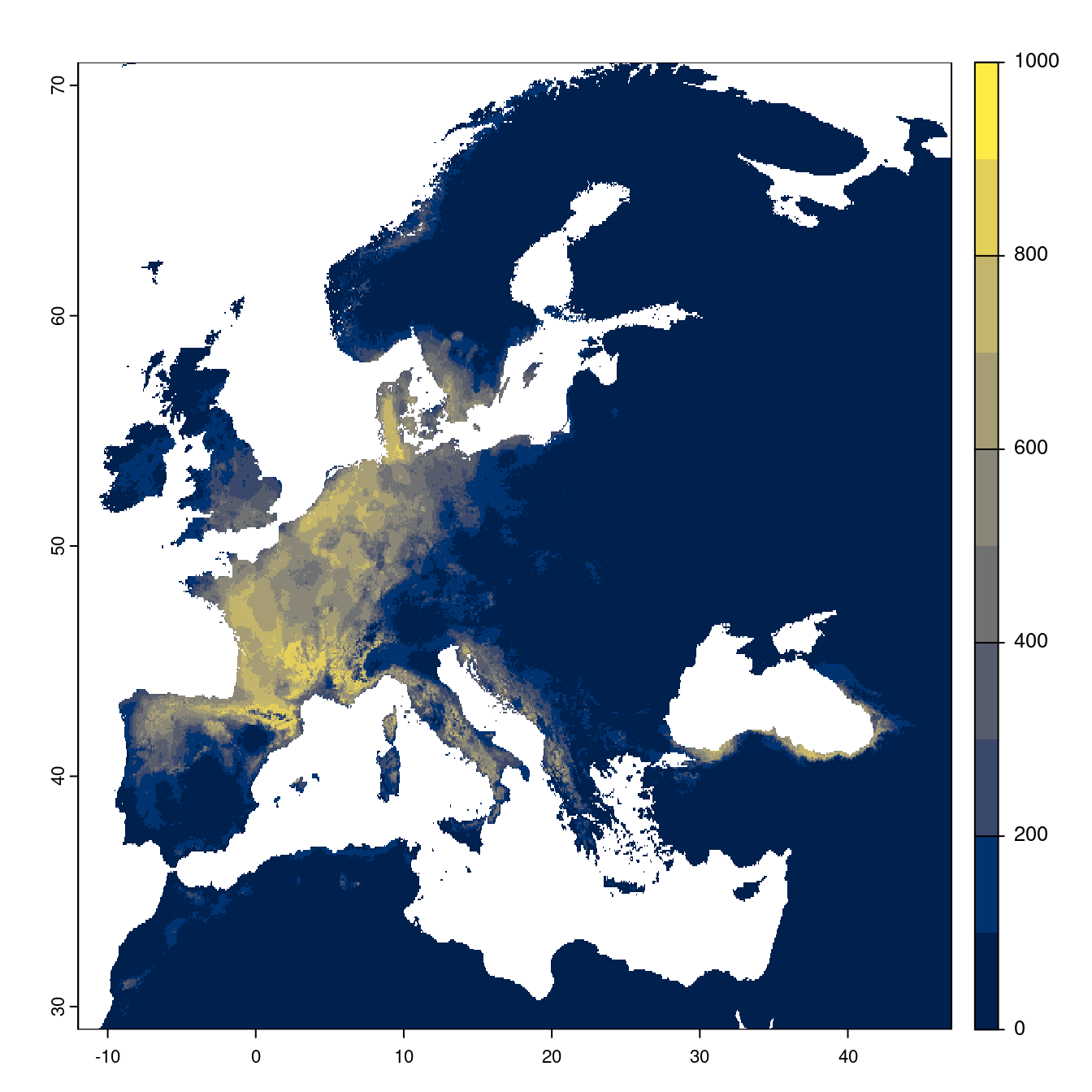
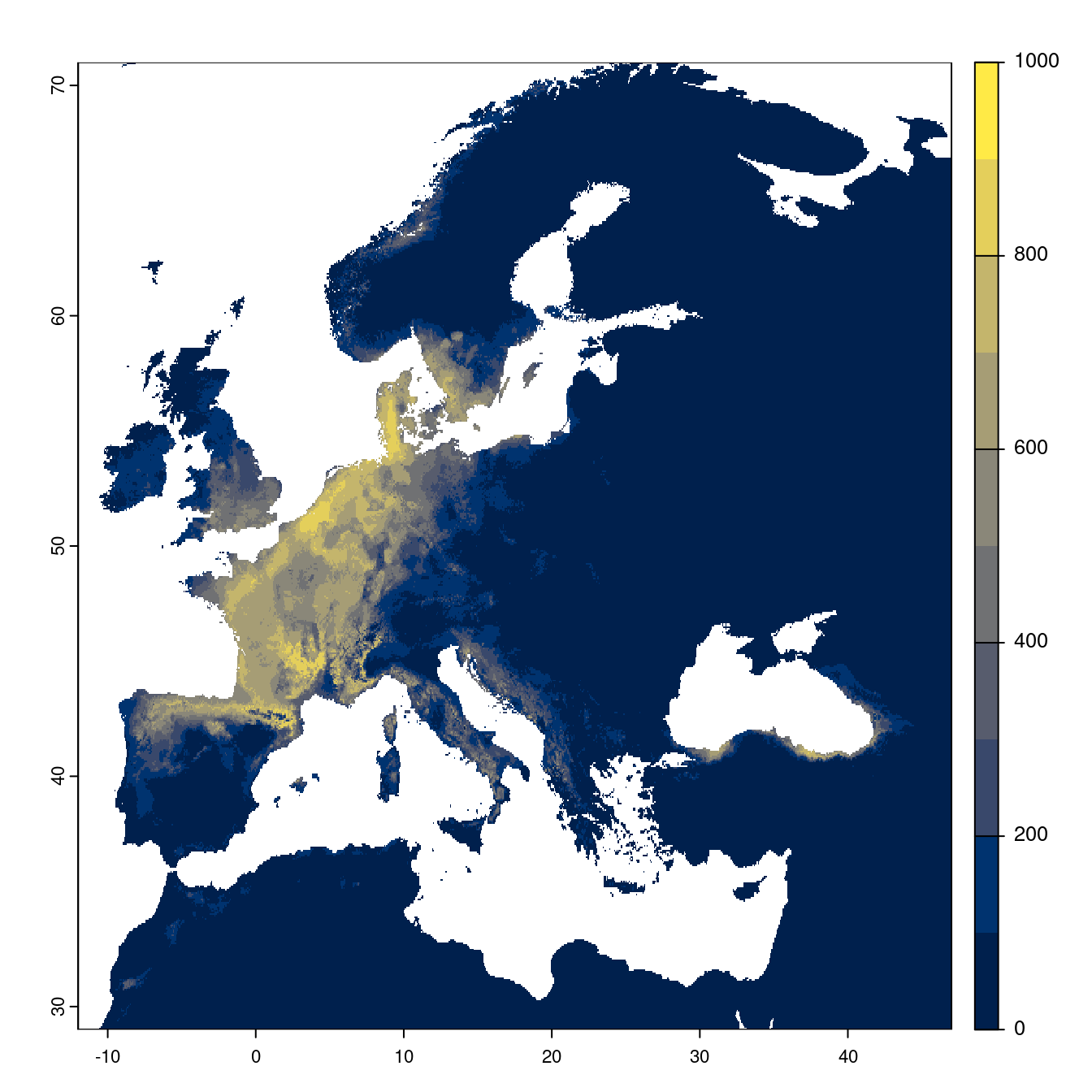
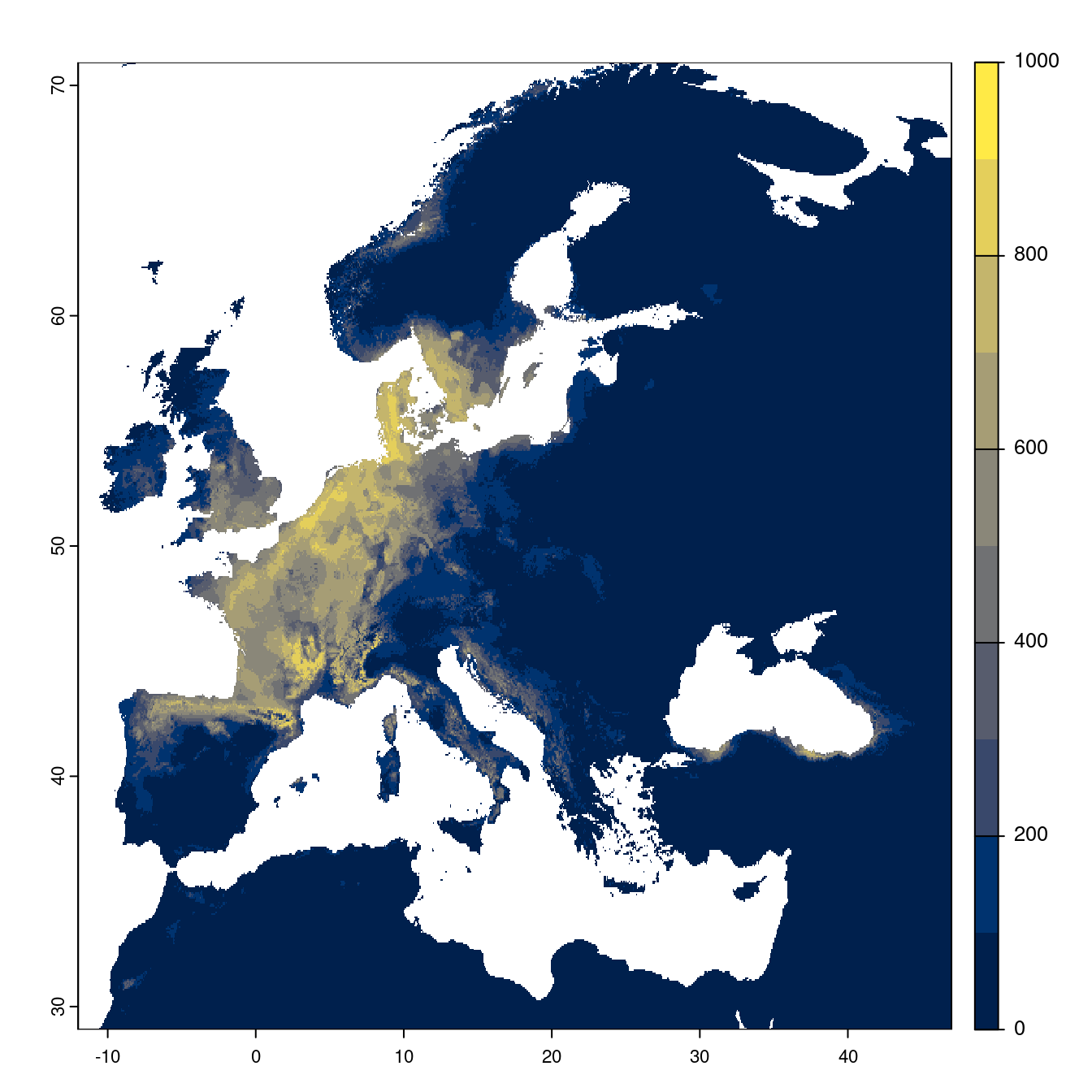
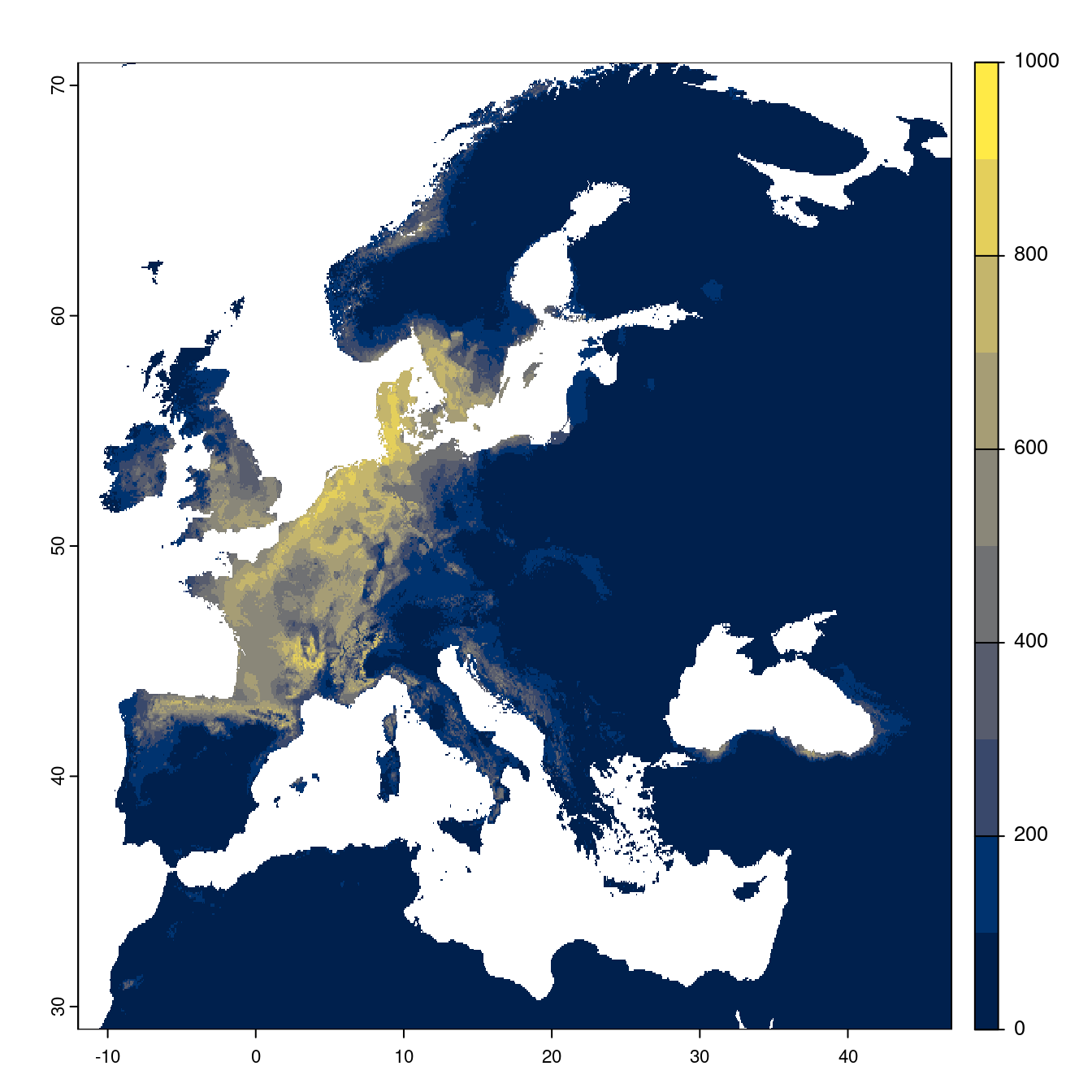
Figure 3.23: Projection des distributions potentielles futures jusqu’à l’horizon 2100 sous le scénario SSP2-4.5 (modèle d’ensemble).
- SSP3-7.0


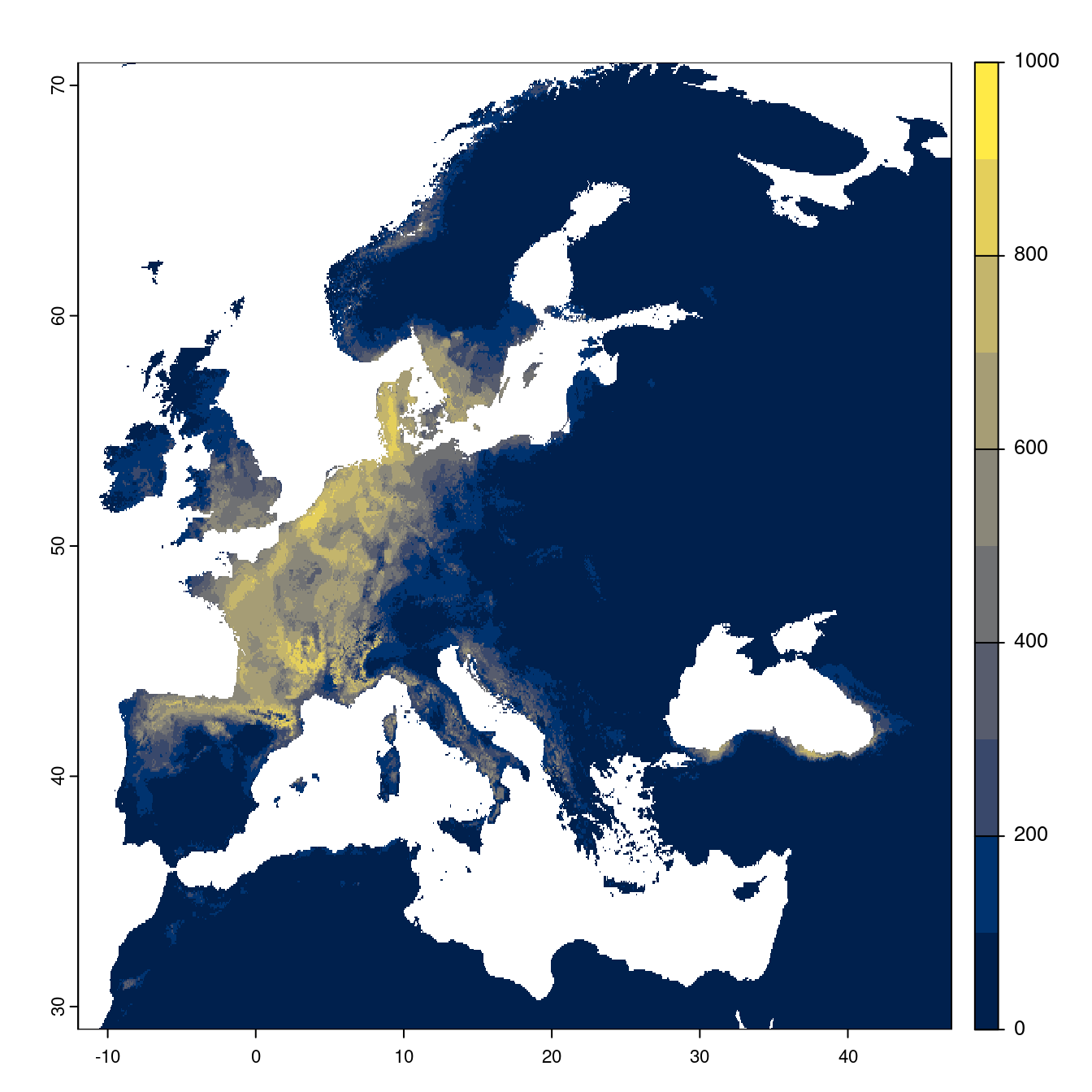
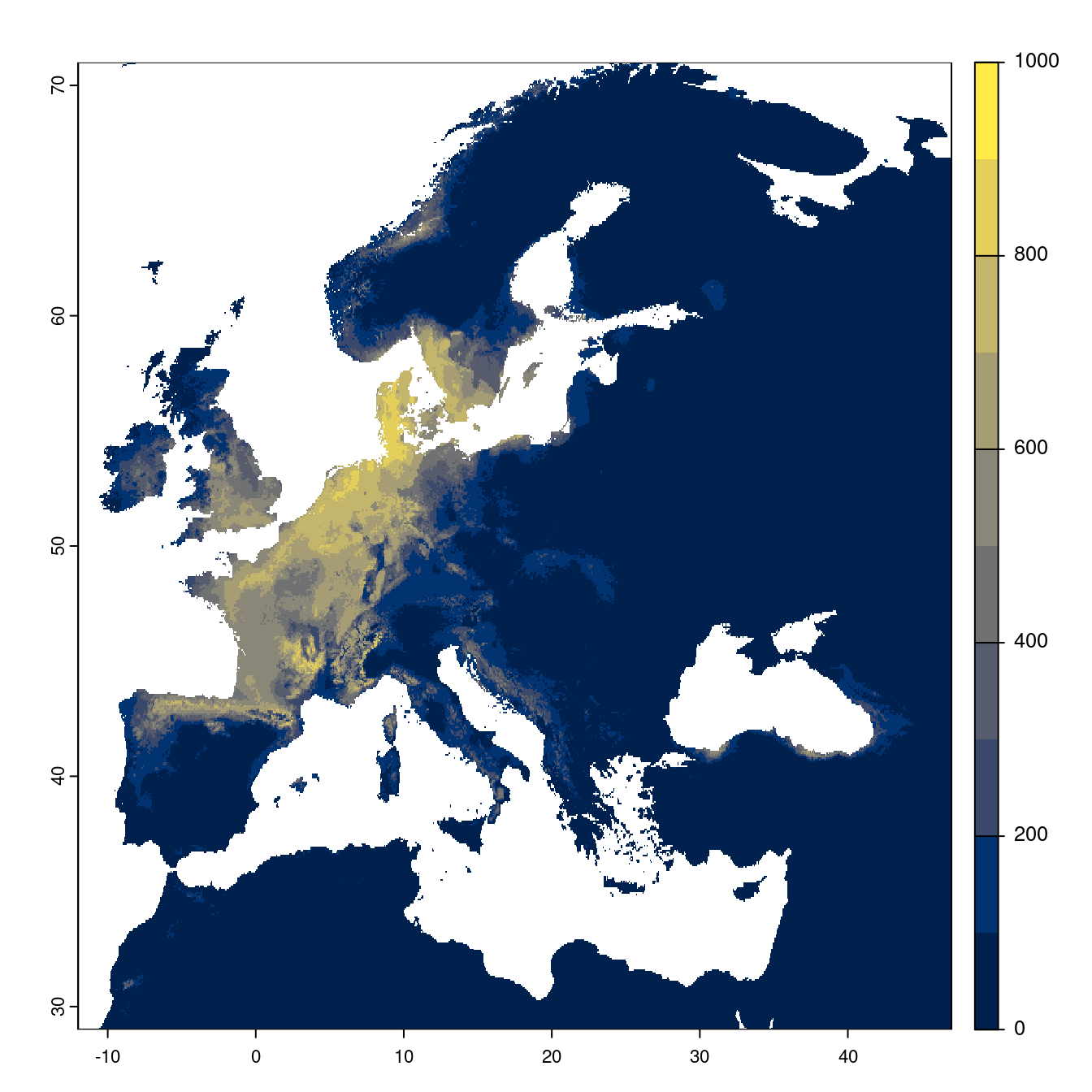
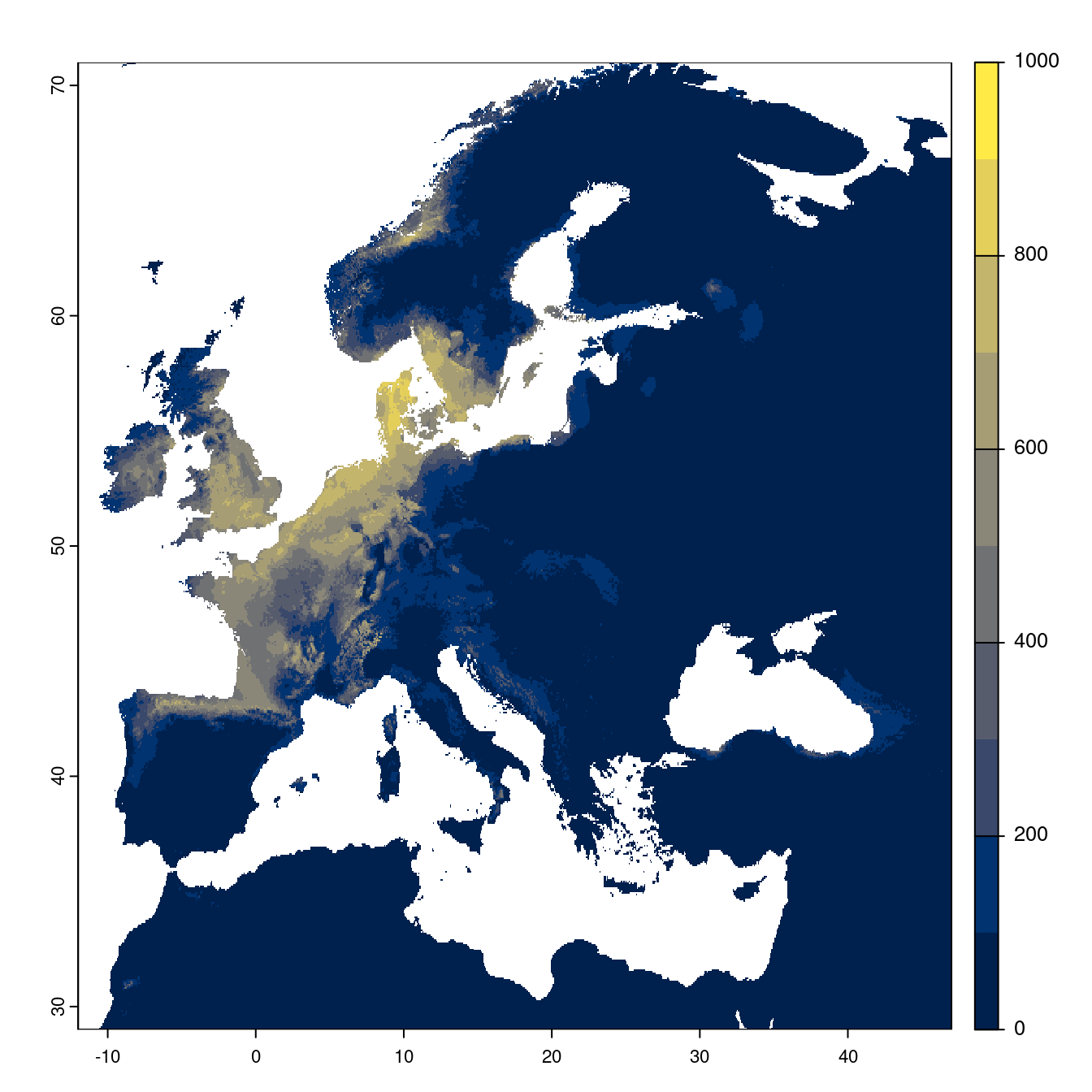
Figure 3.24: Projection des distributions potentielles futures jusqu’à l’horizon 2100 sous le scénario SSP3-7.0 (modèle d’ensemble).
- SSP5-8.5
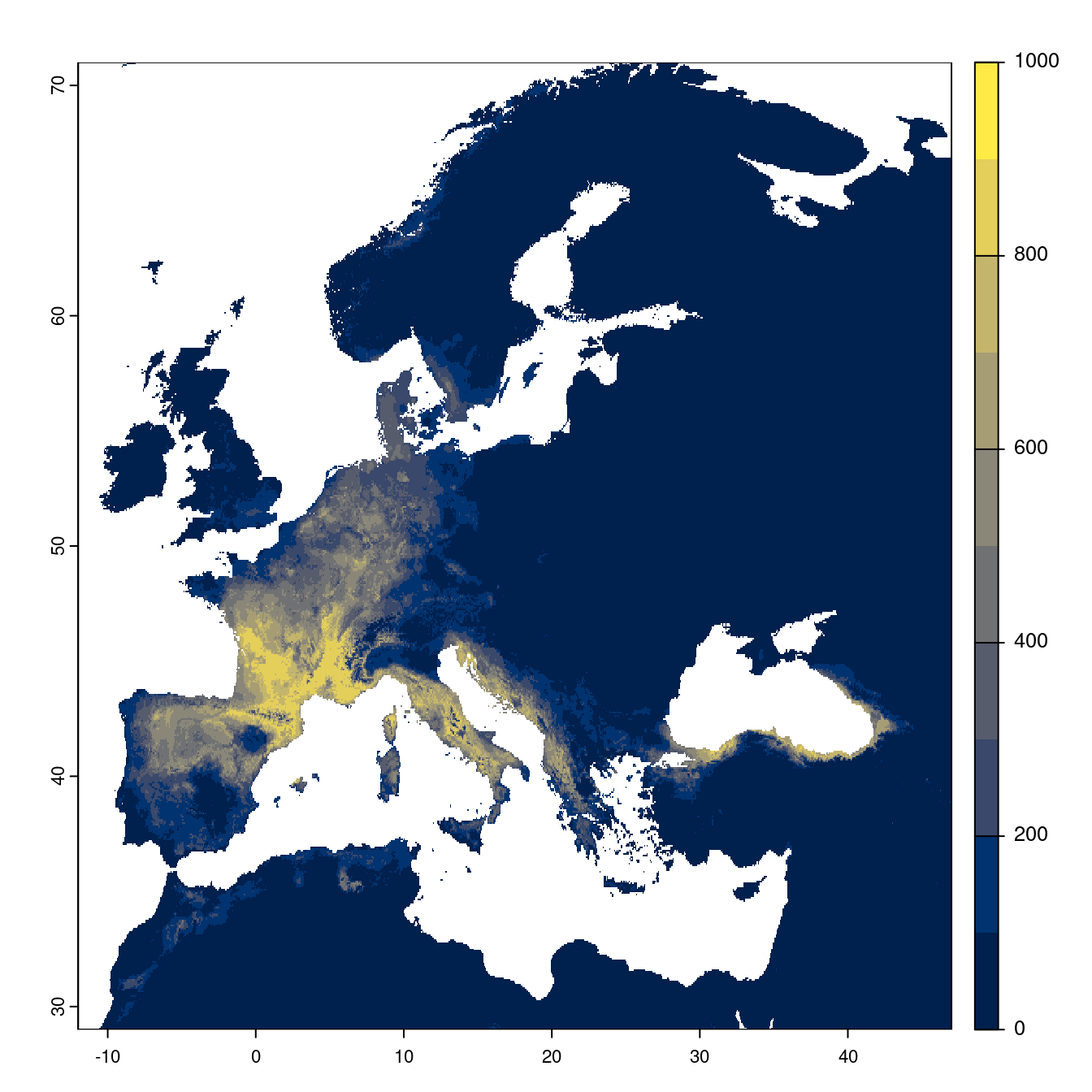
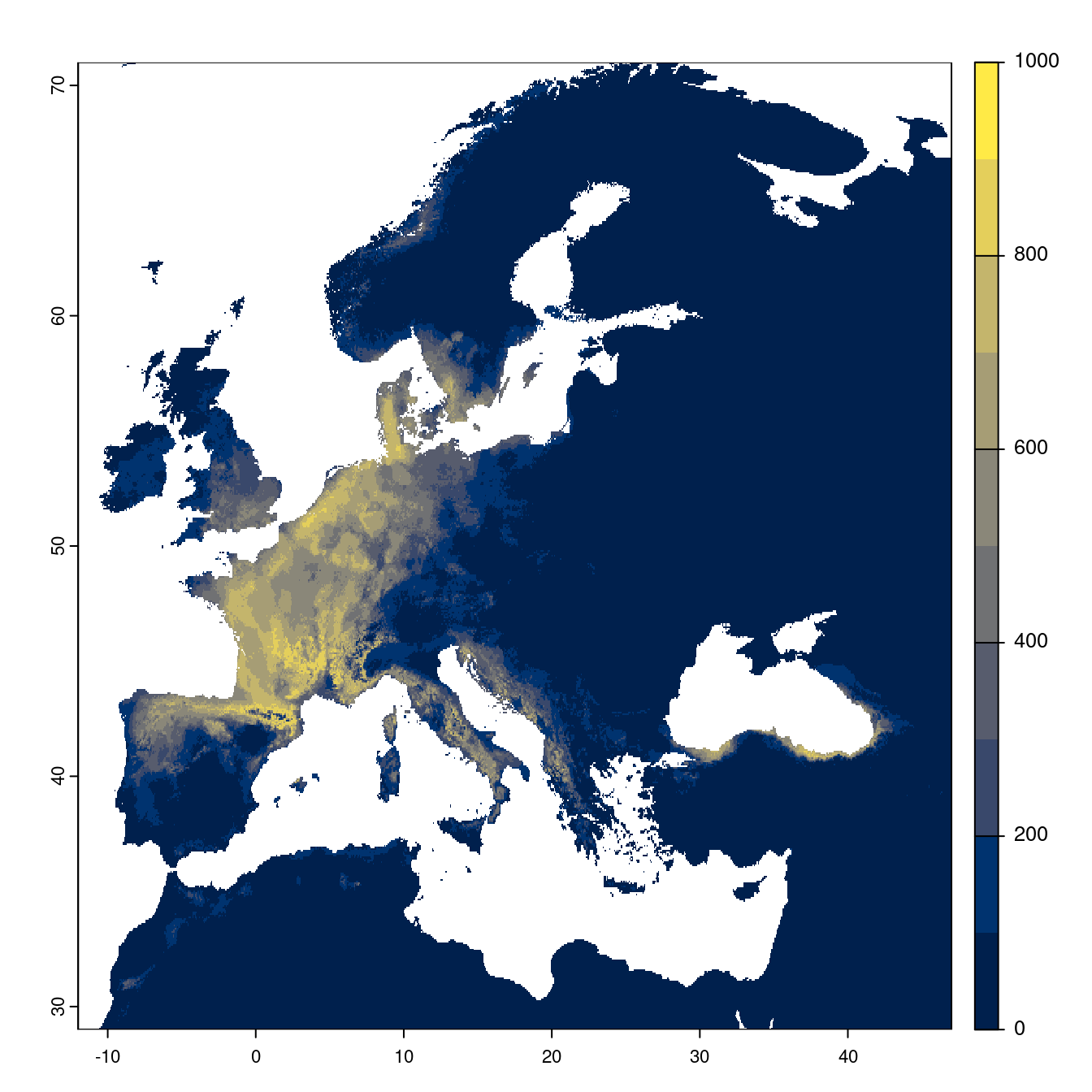
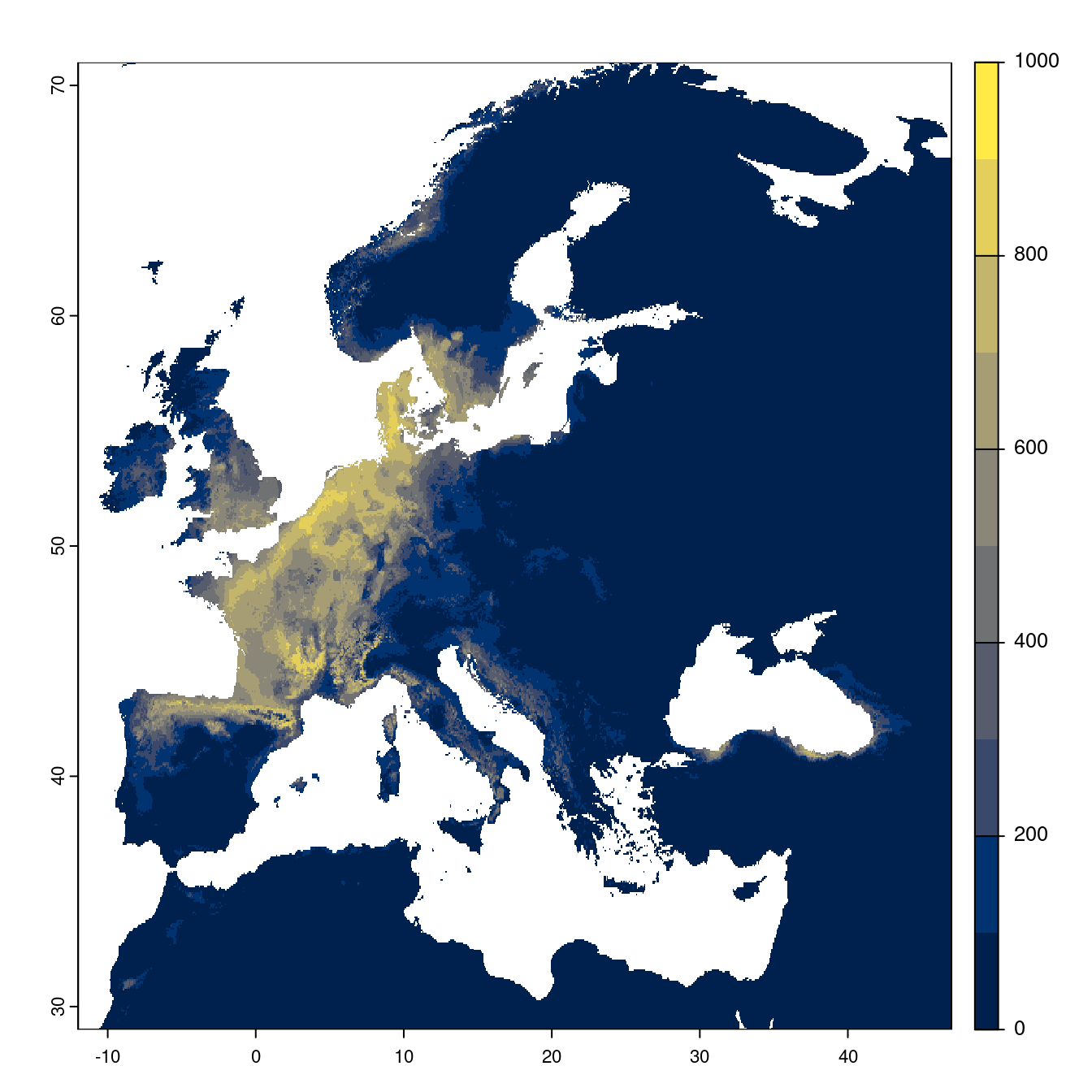
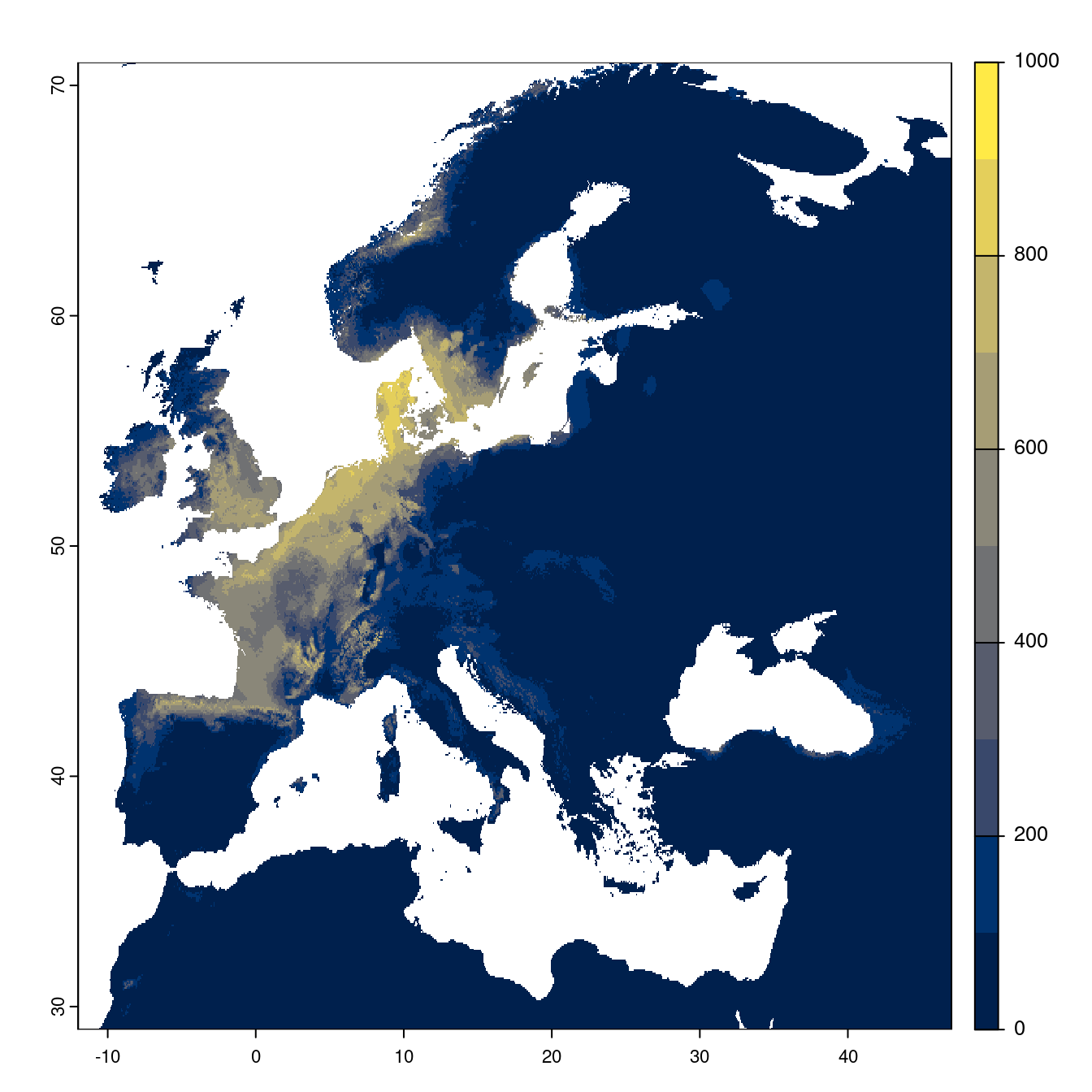
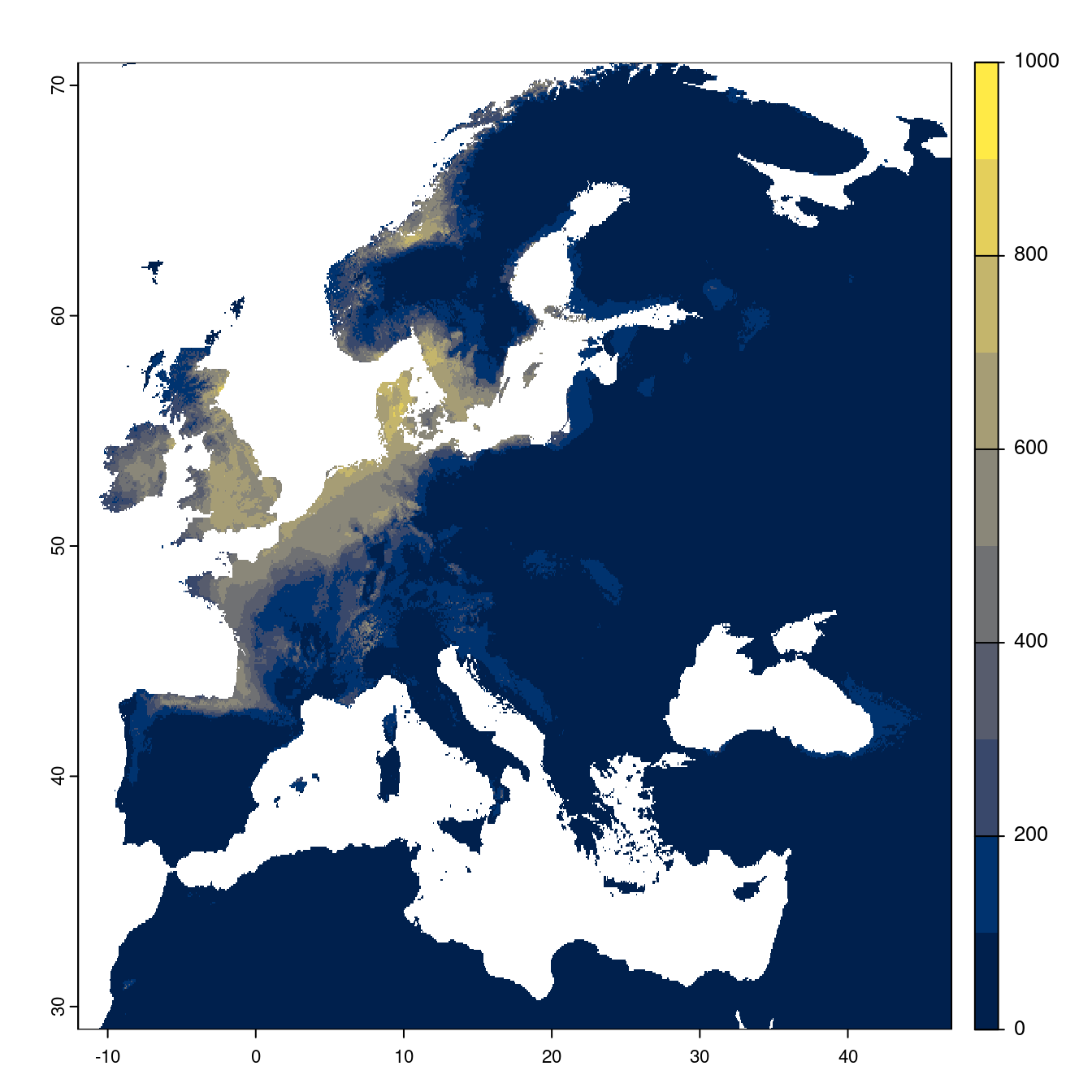
Figure 3.25: Projection des distributions potentielles futures jusqu’à l’horizon 2100 sous le scénario SSP5-8.5 (modèle d’ensemble).
3.6 Inférence à l’échelle de la métropole
- Espèces potentielles pour Grenoble (forte probabilité de présence à l’horizon 2100)
- Croisement avec températures de surface 2019 (fournie par la métropole)
- → conditions climatiques favorables à fine échelle
à peu près 7 pixels × 9 (WorldClim)
3.6.1 Distributions potentielles futures
Même chose que précédemment mais sur les rasters de Grenoble
- SSP1-2.6

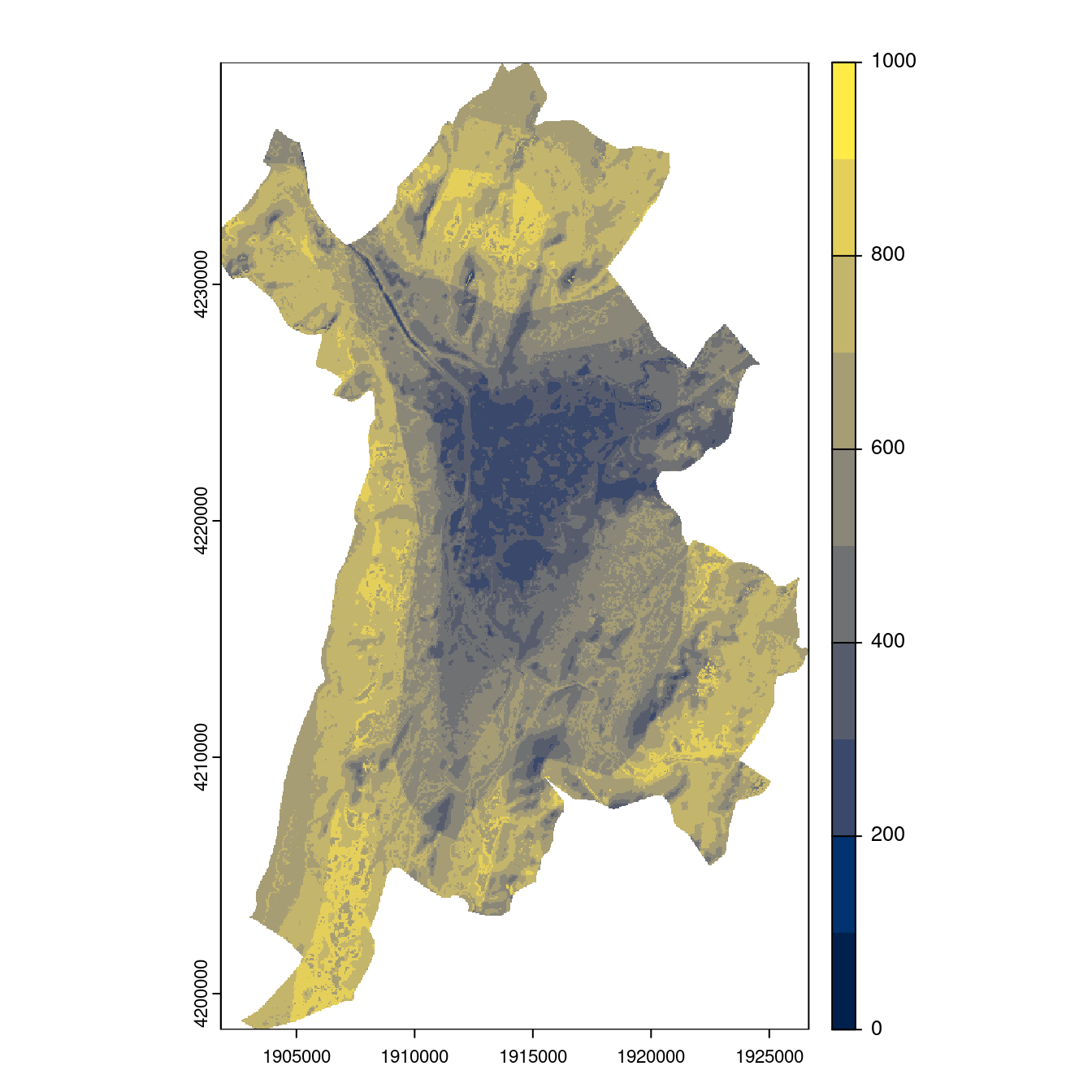

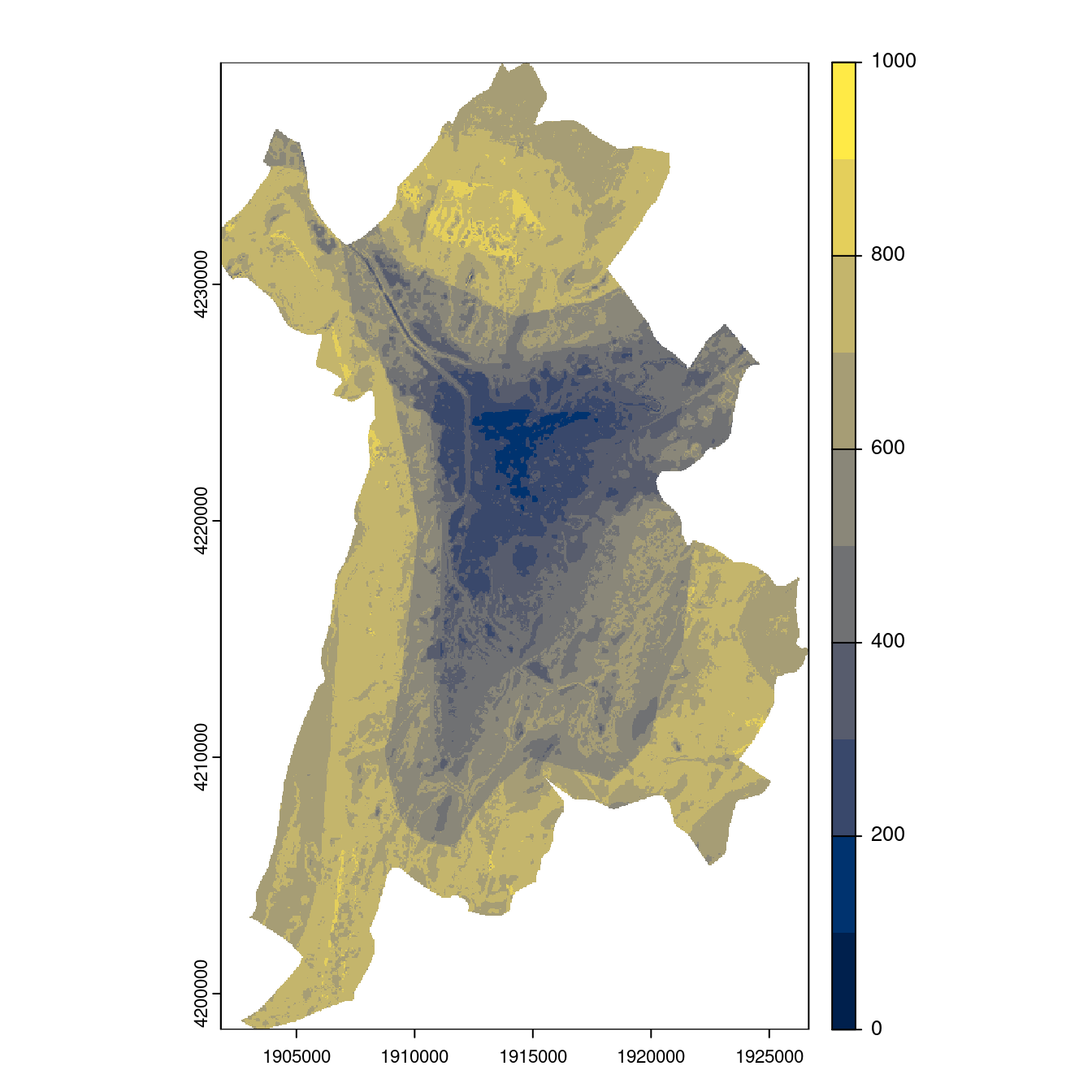
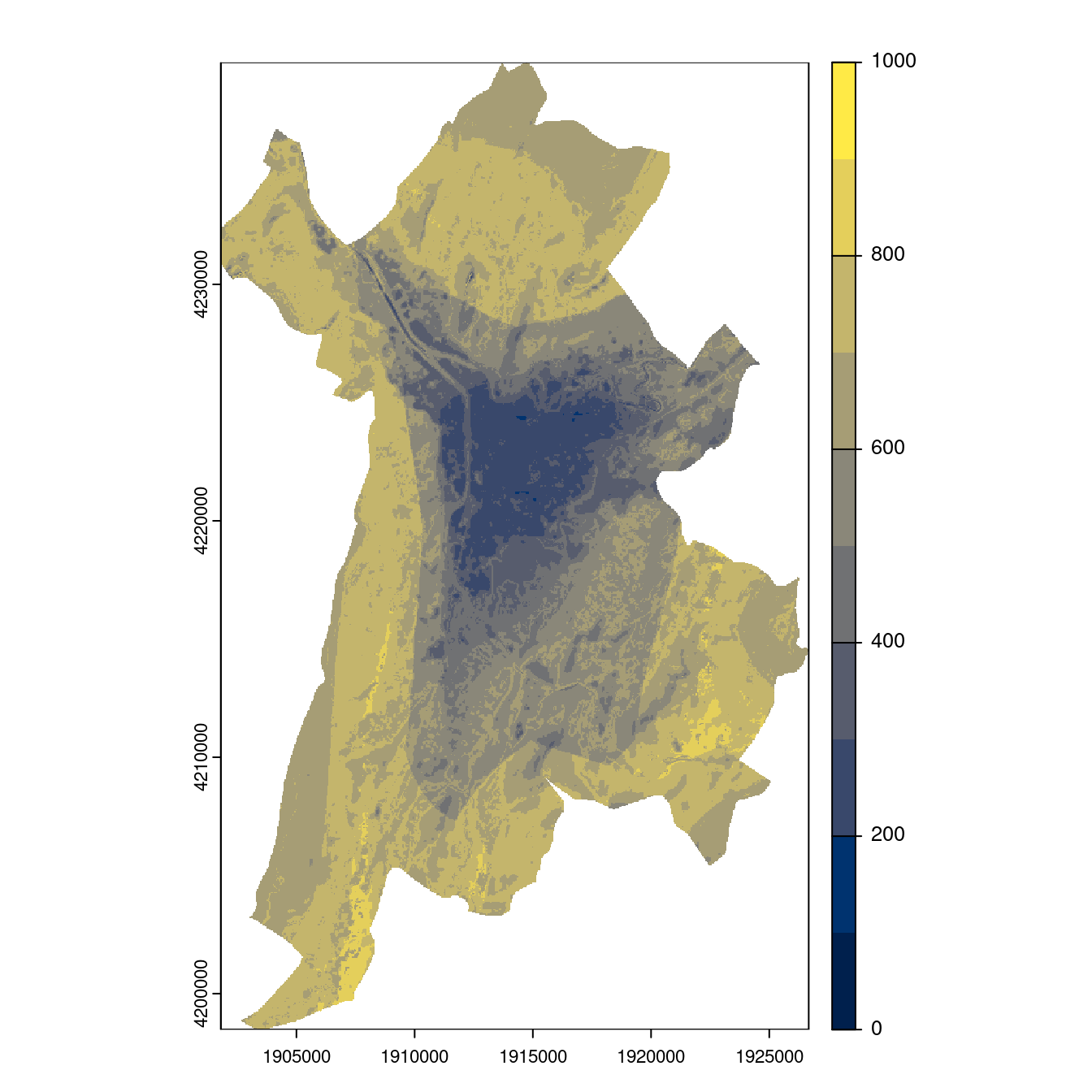
Figure 3.26: Projection des distributions potentielles contemporaine et futures jusqu’à l’horizon 2100 sous le scénario SSP5-8.5 (modèle d’ensemble, GCM IPSL).
- SSP2-4.5
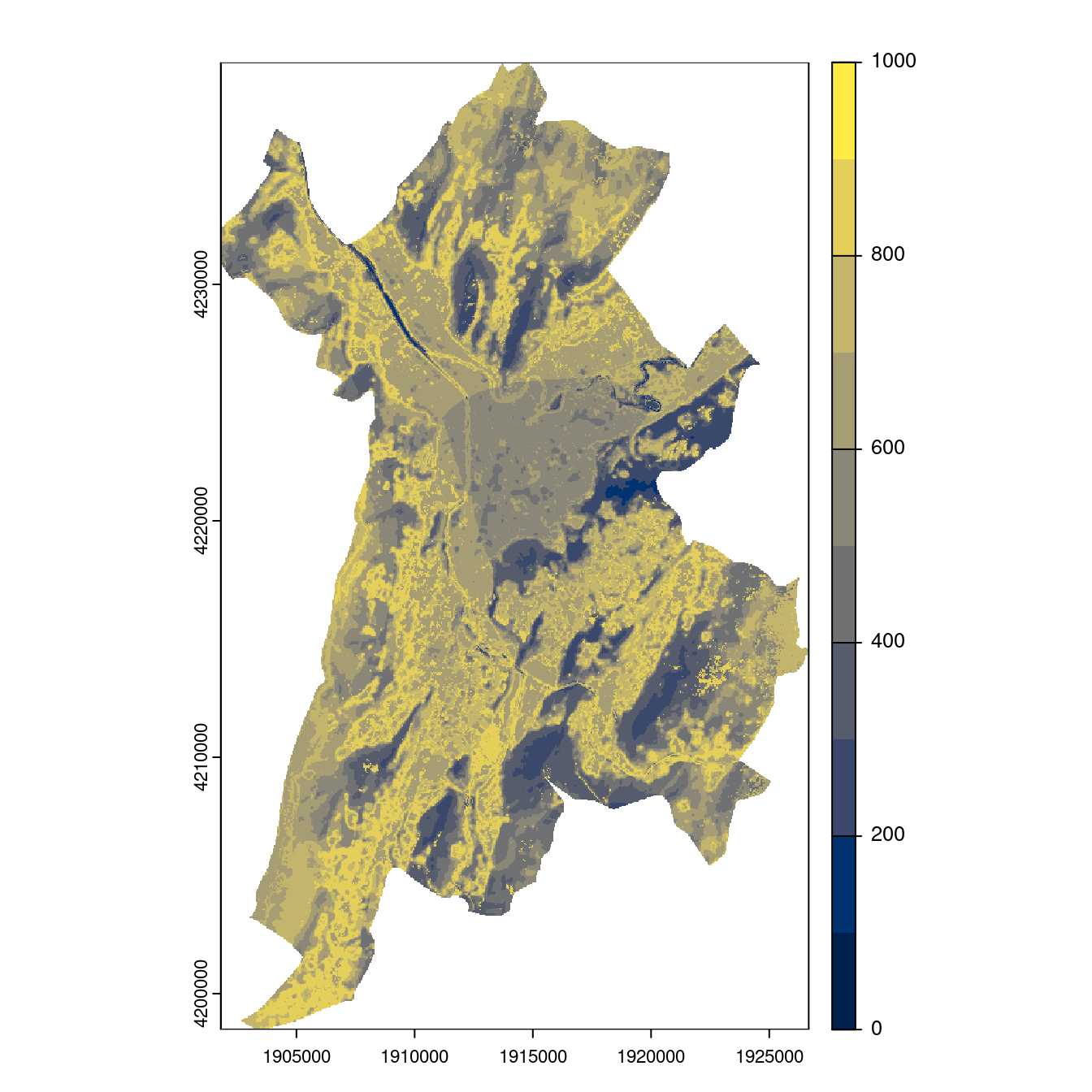
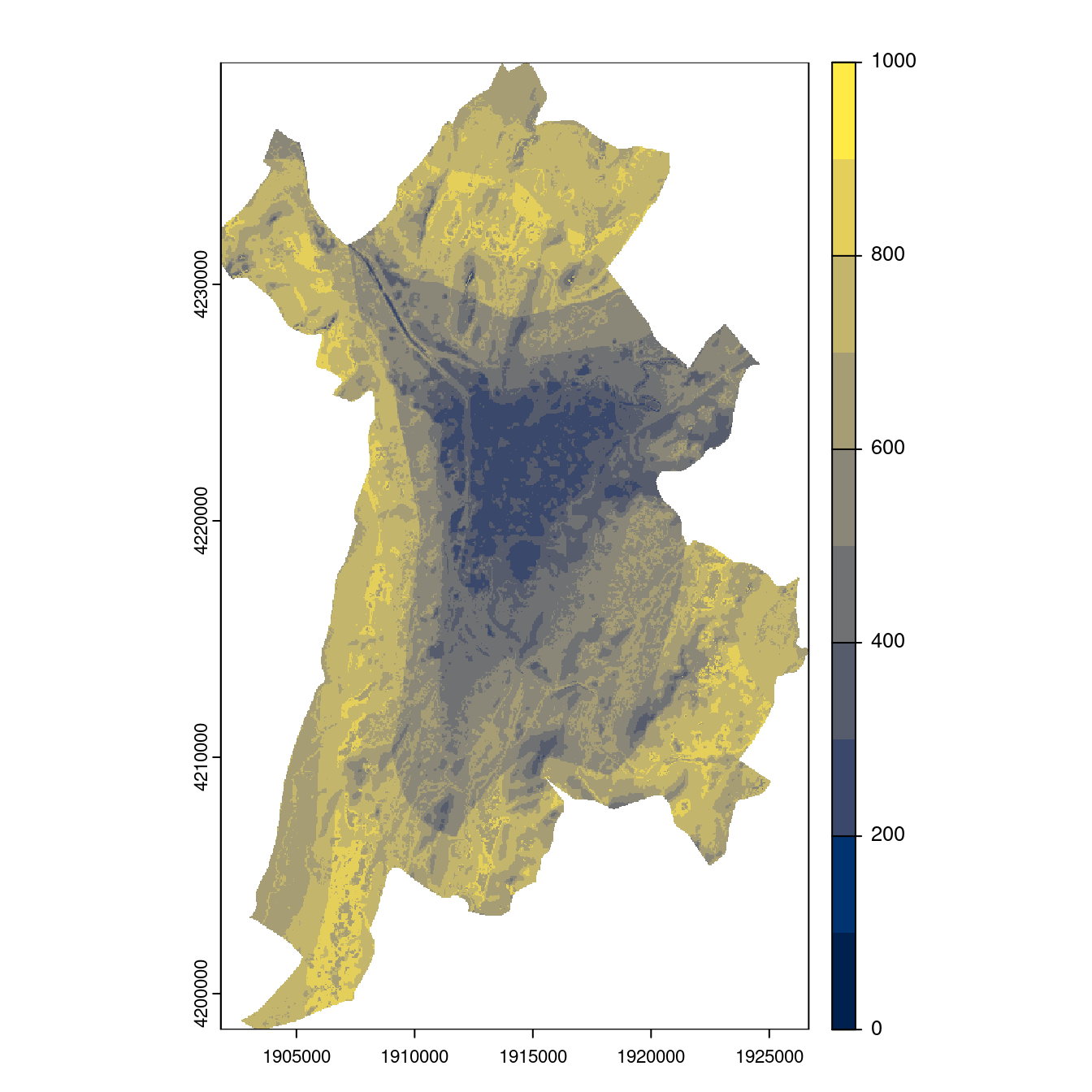
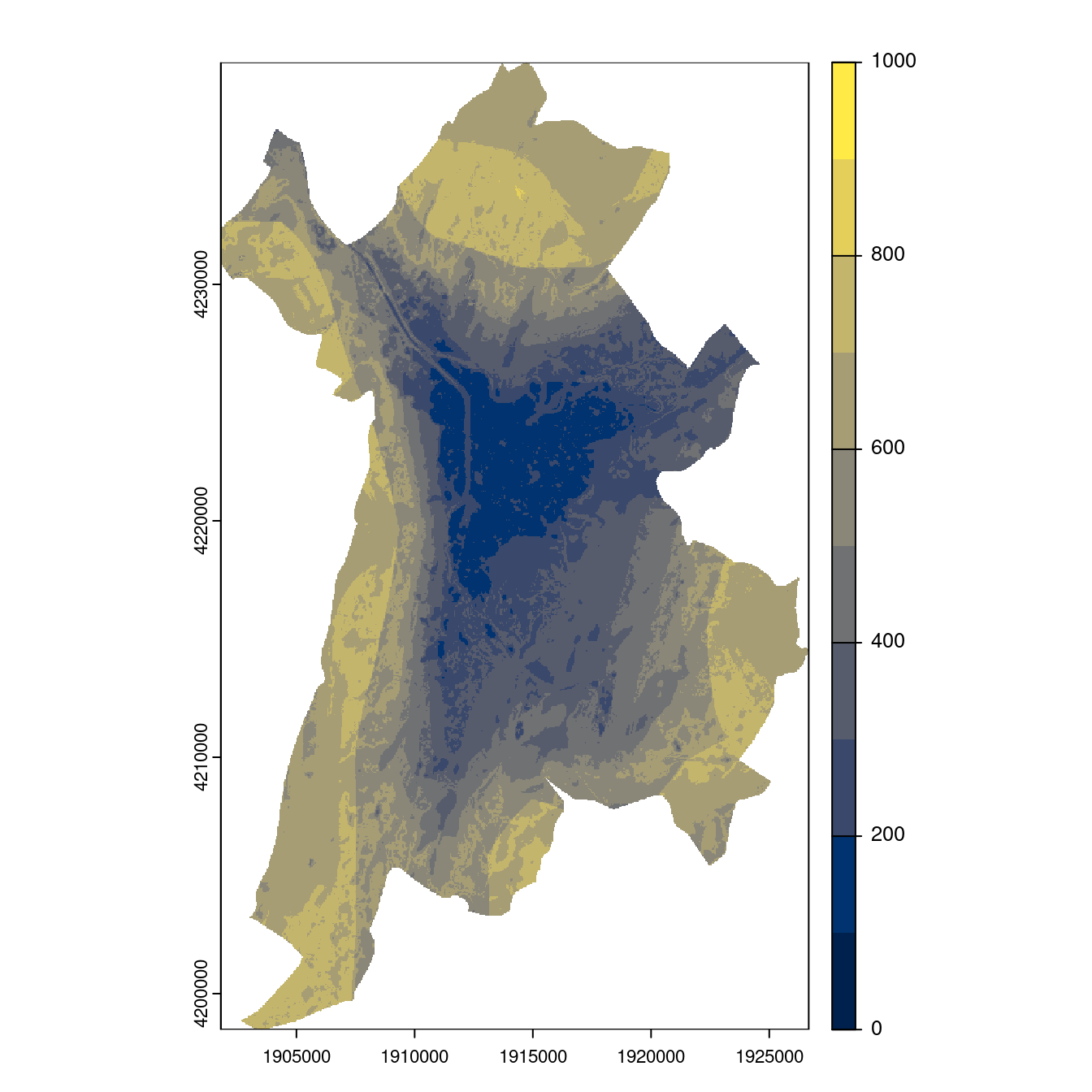
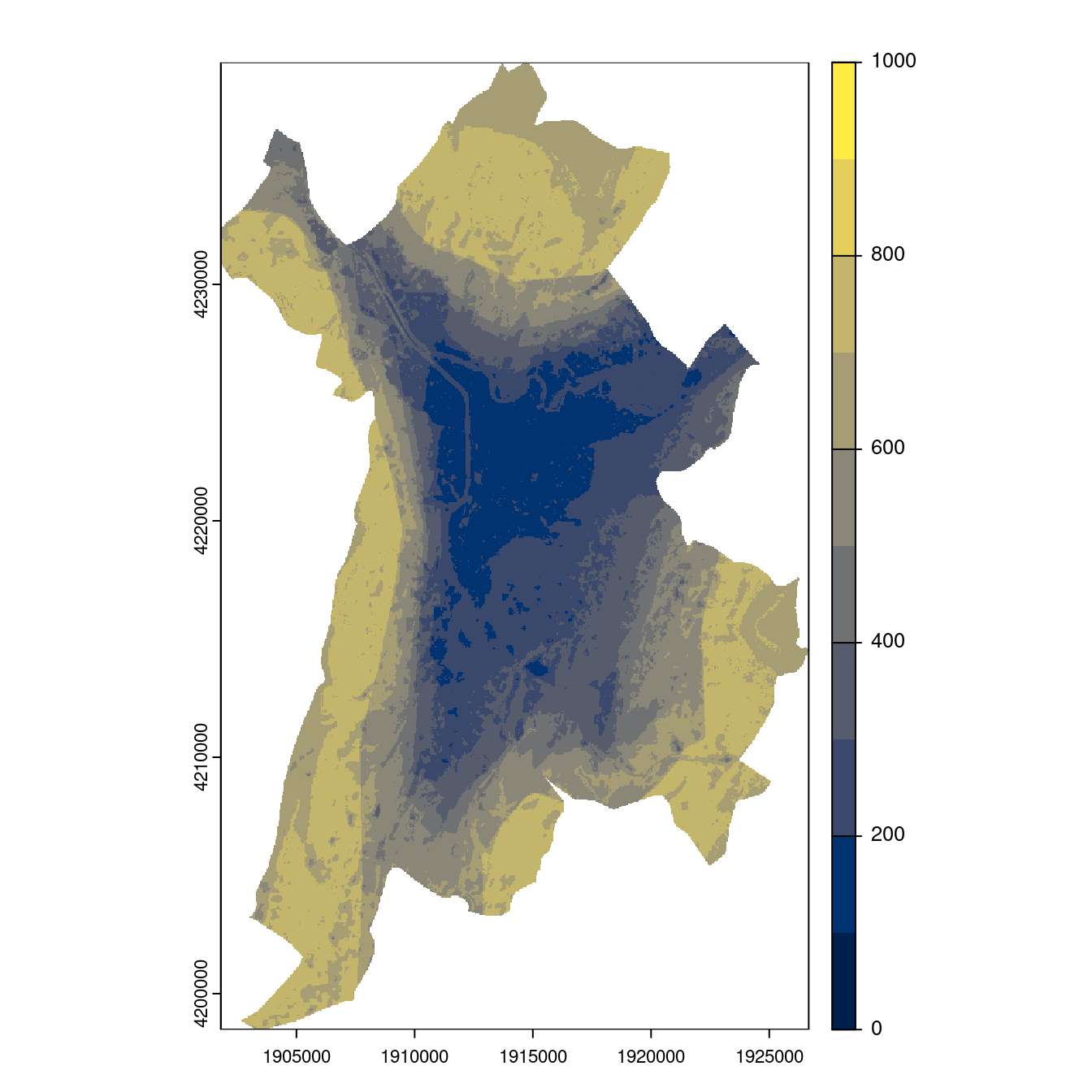
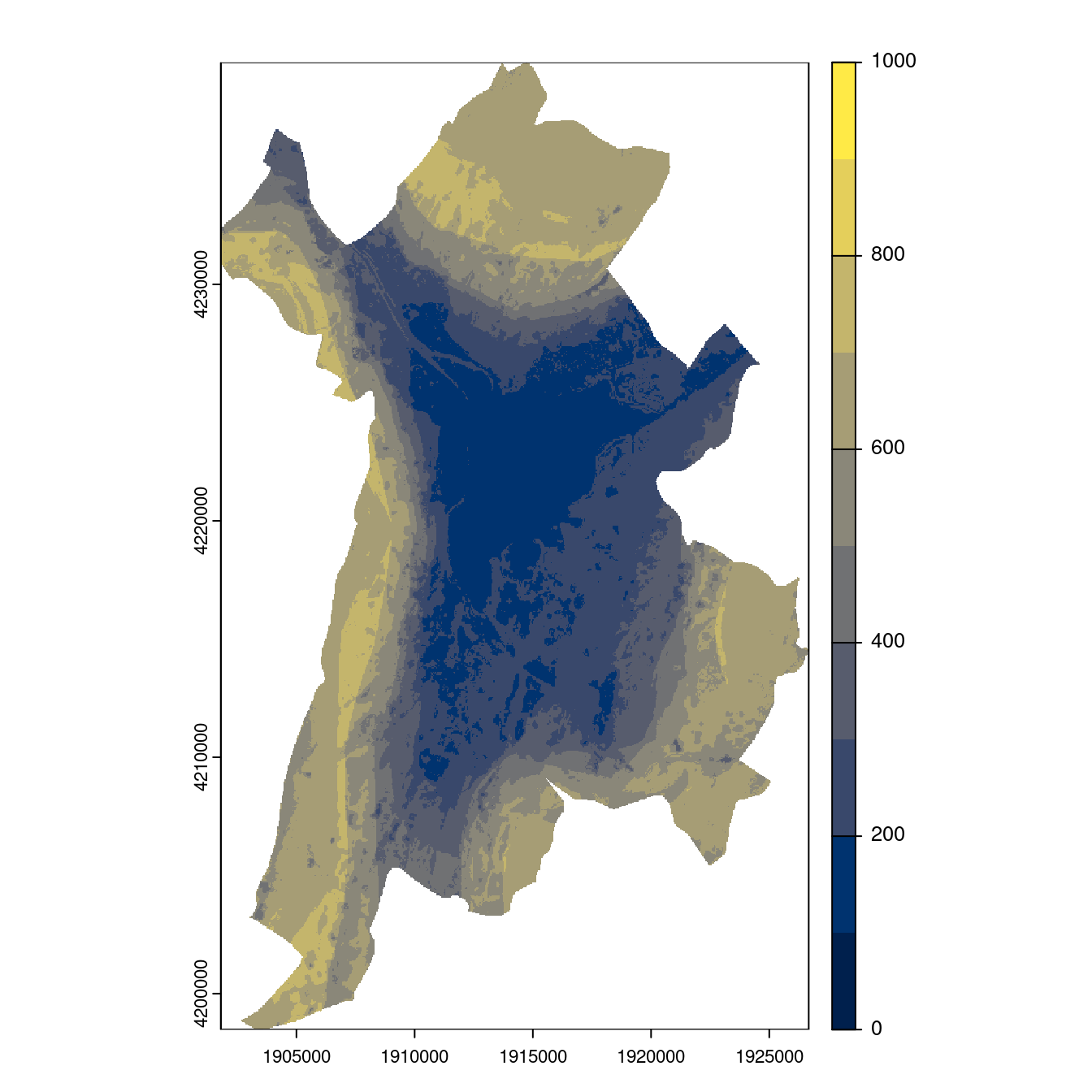
Figure 3.27: Projection des distributions potentielles contemporaine et futures jusqu’à l’horizon 2100 sous le scénario SSP5-8.5 (modèle d’ensemble, GCM IPSL).
- SSP3-7.0
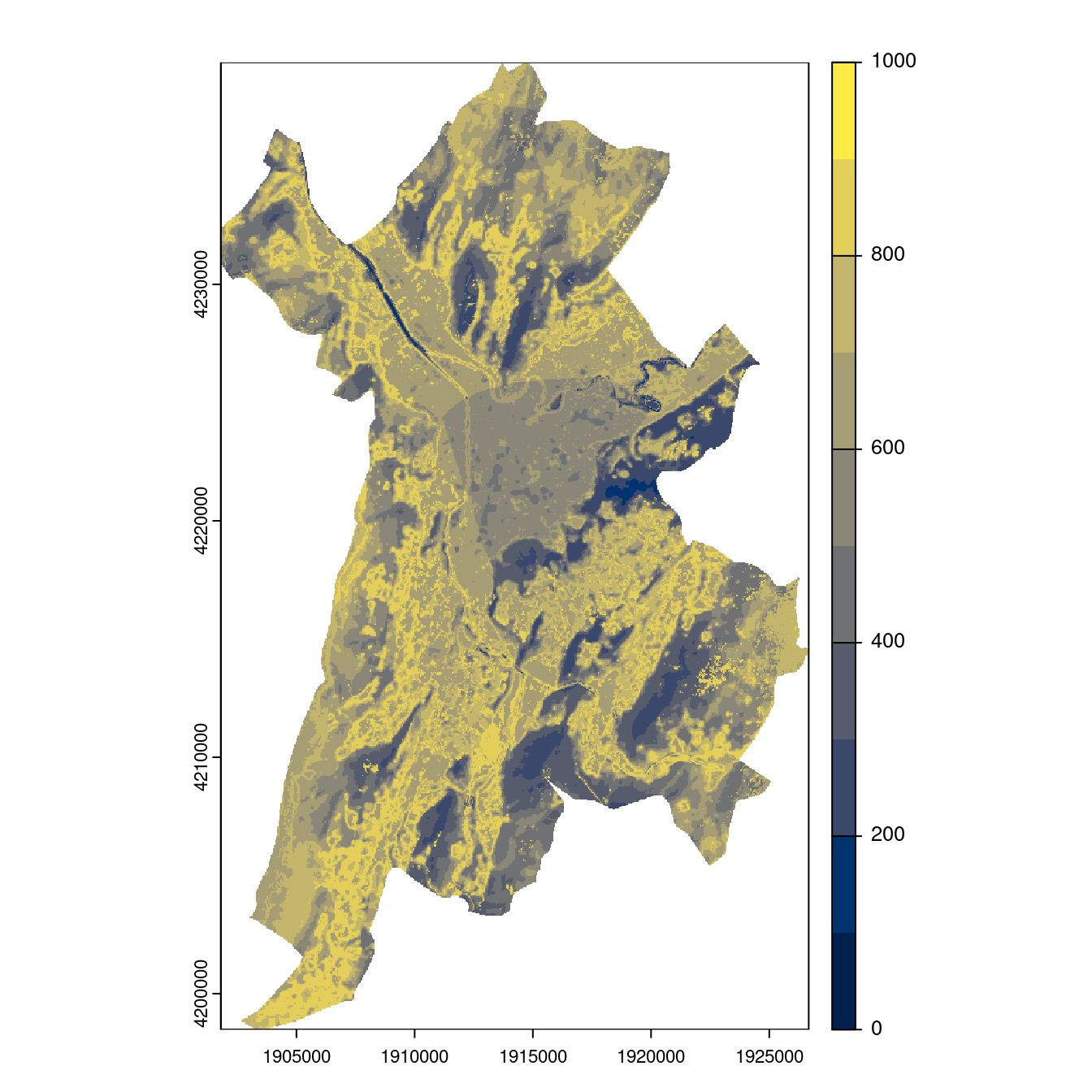
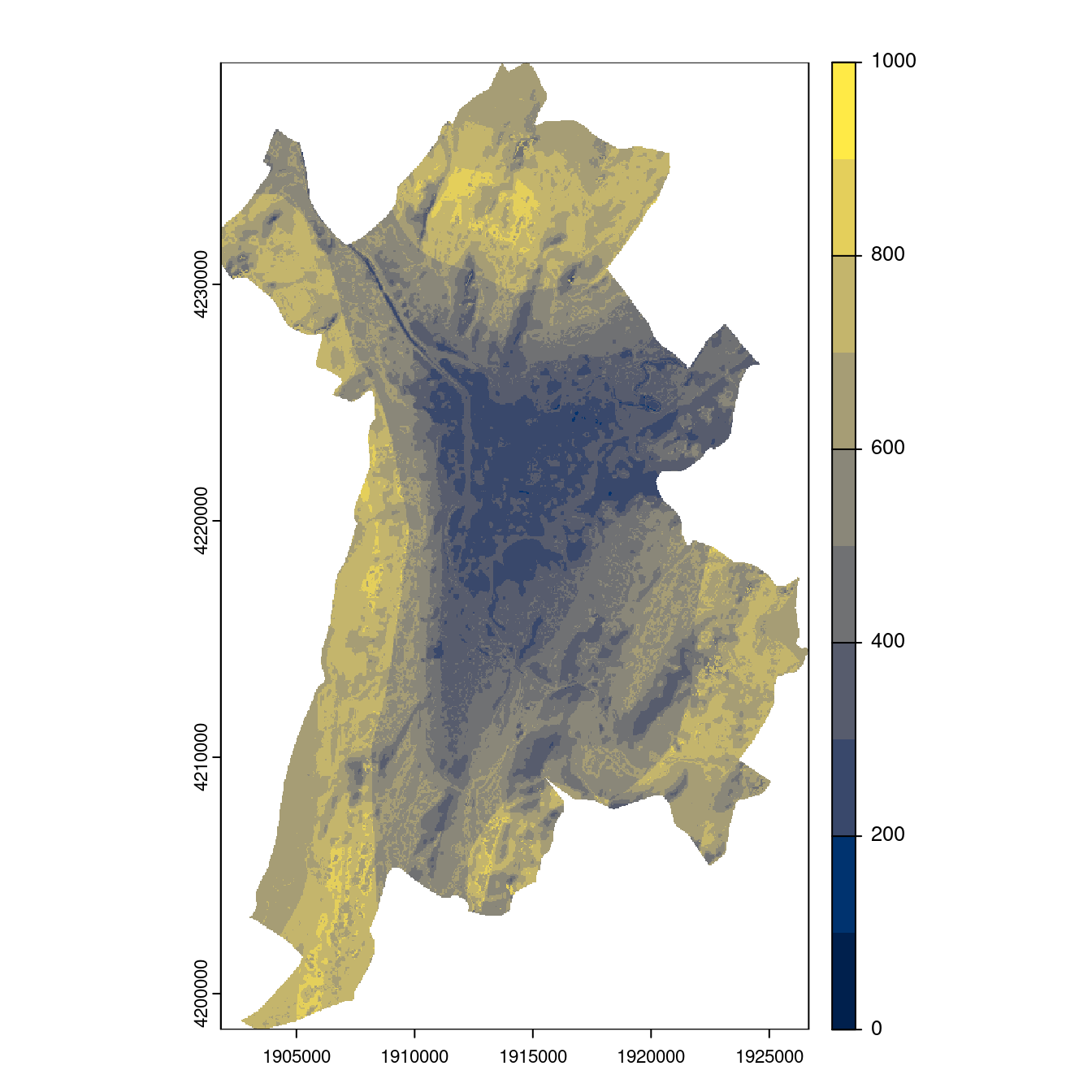
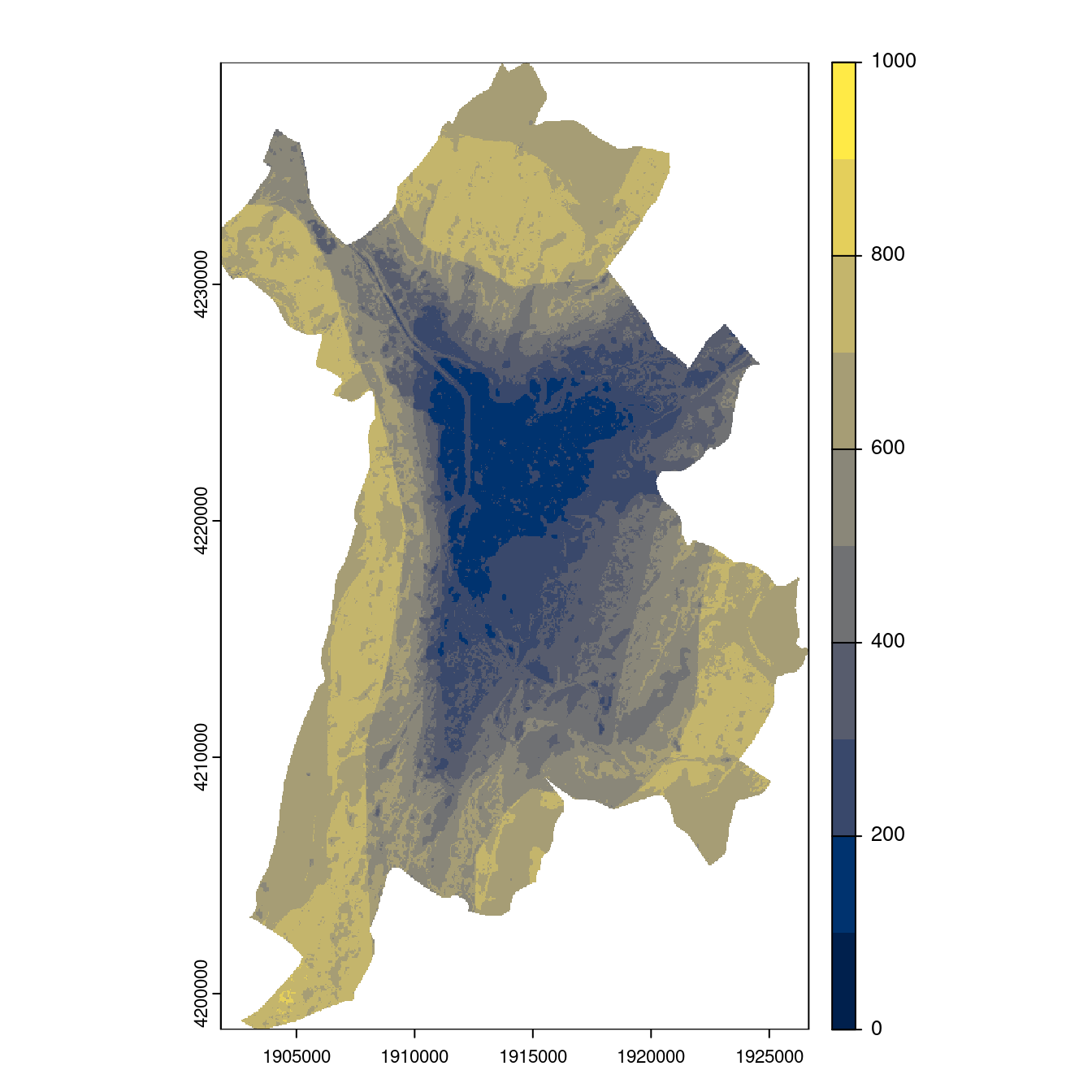
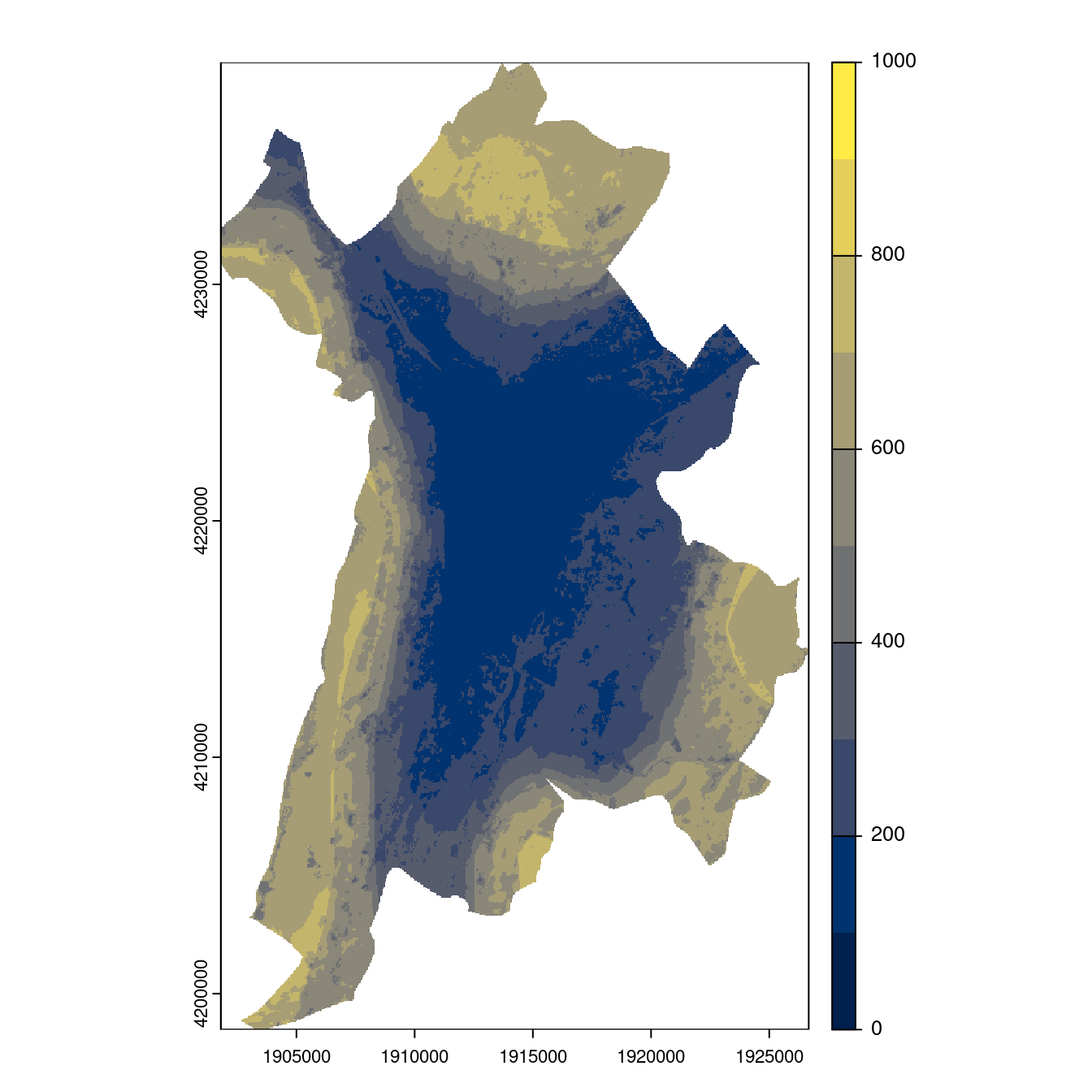
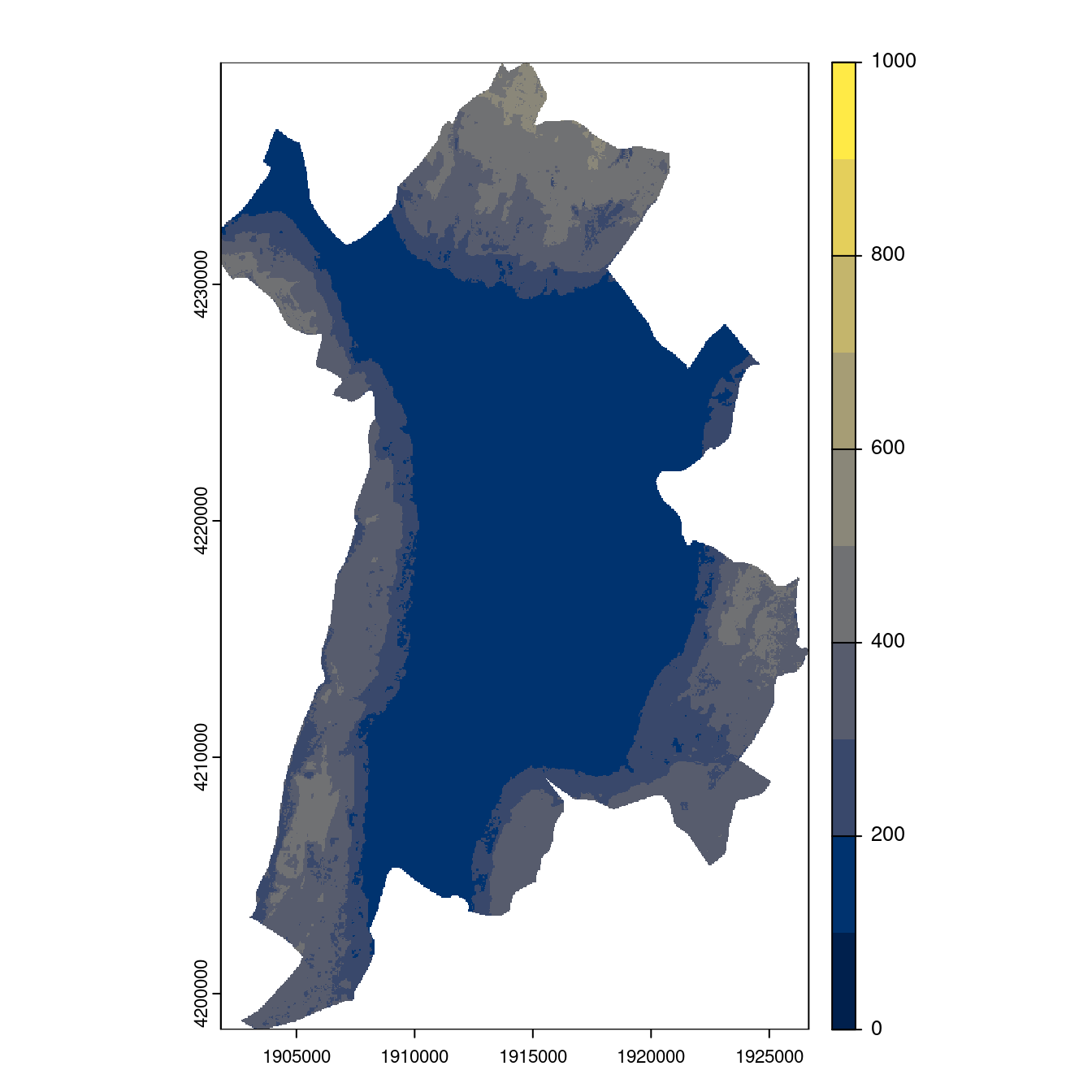
Figure 3.28: Projection des distributions potentielles contemporaine et futures jusqu’à l’horizon 2100 sous le scénario SSP5-8.5 (modèle d’ensemble, GCM IPSL).
- SSP5-8.5
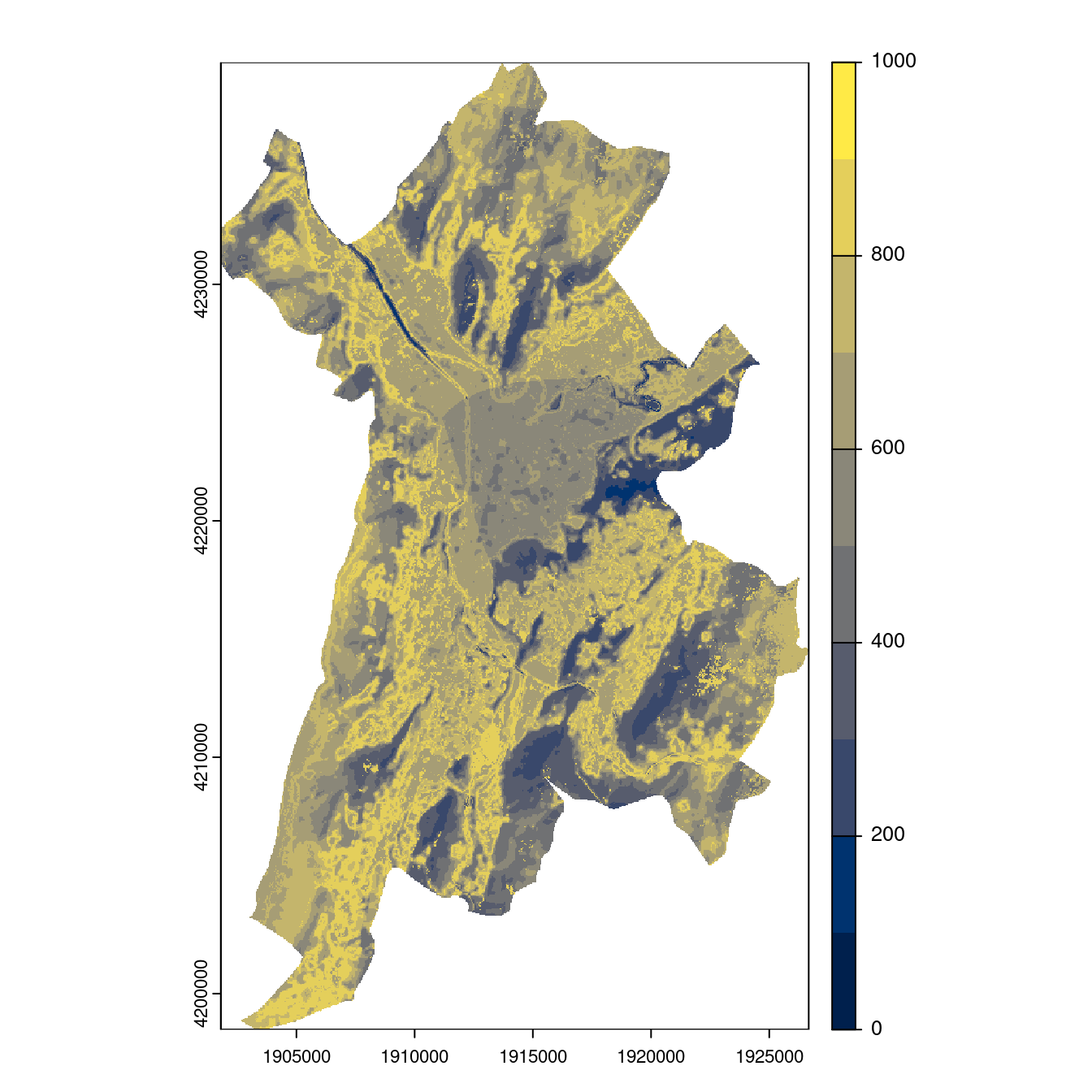
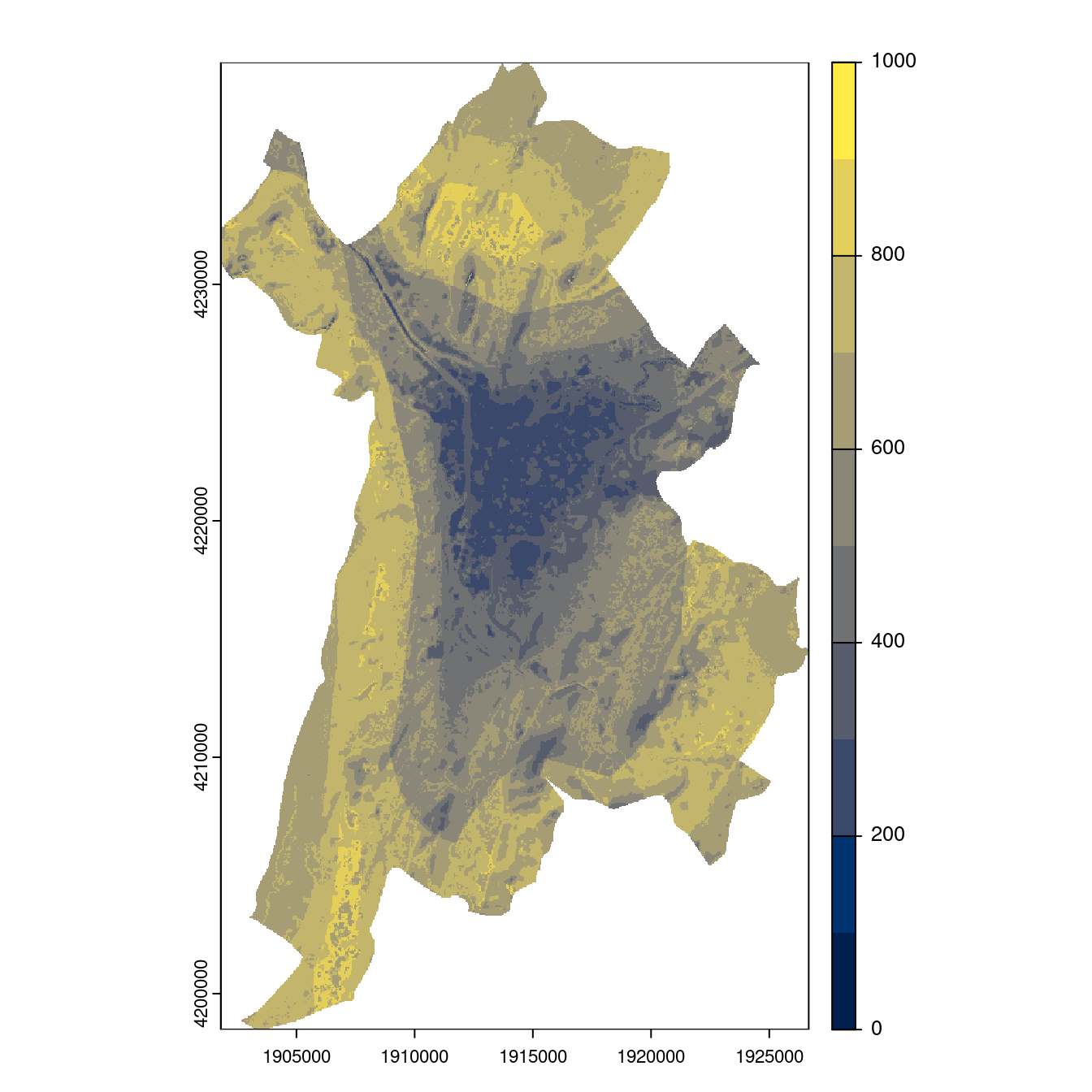

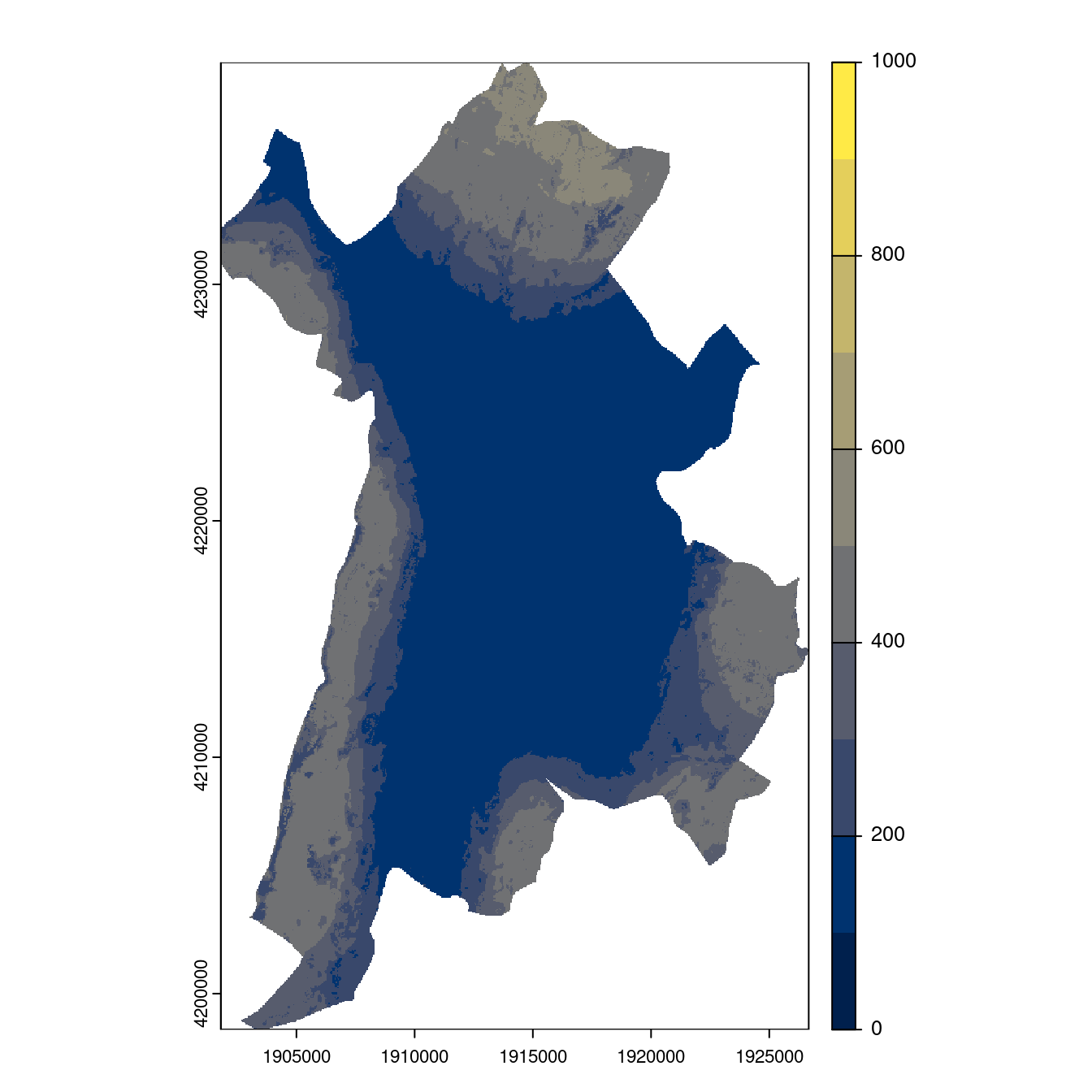
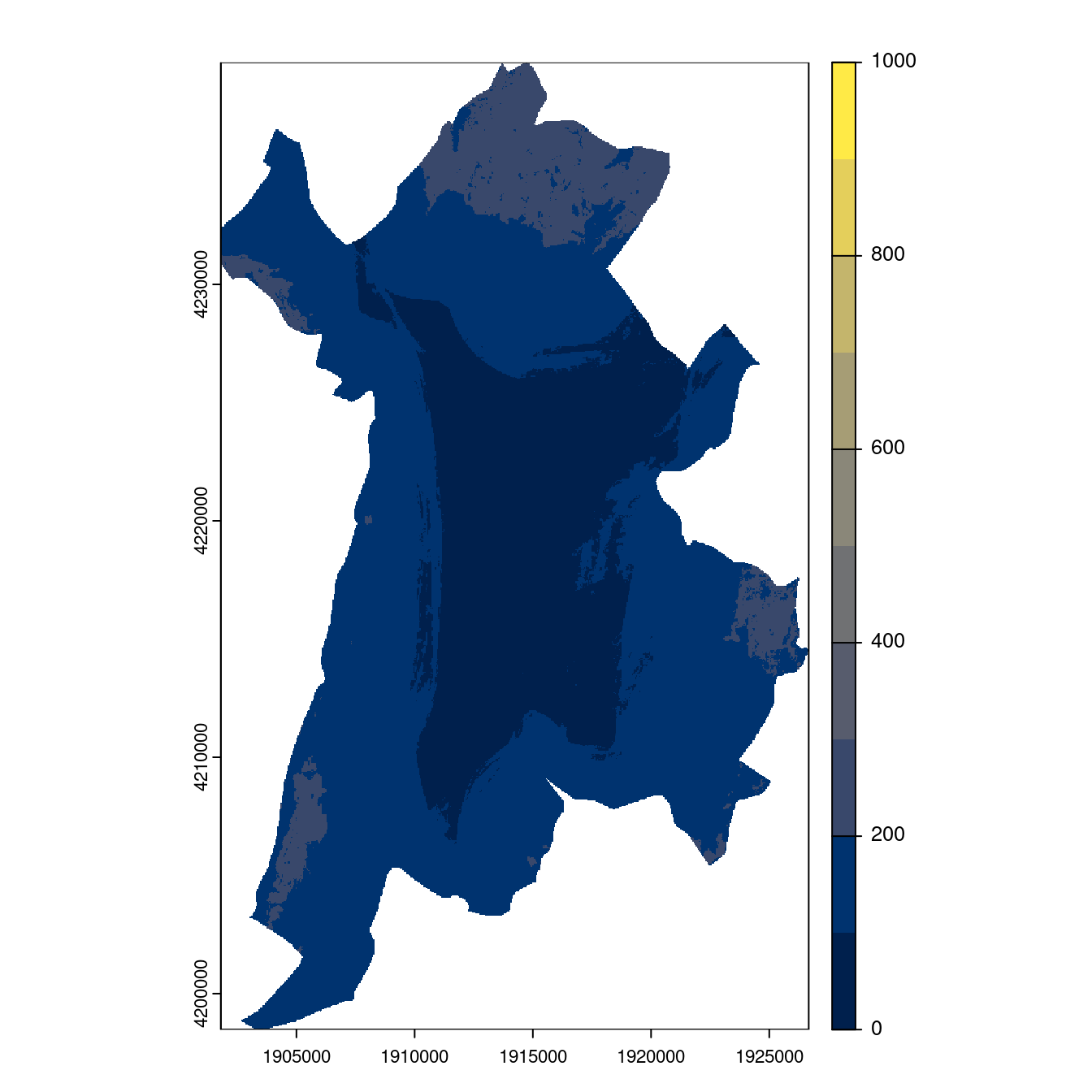
Figure 3.29: Projection des distributions potentielles contemporaine et futures jusqu’à l’horizon 2100 sous le scénario SSP5-8.5 (modèle d’ensemble, GCM IPSL).
3.6.2 Évolution temporelle
# A tibble: 17 × 8
min q1 median mean q3 max ssp year
<table[1d]> <table[1d]> <table[1d]> <table[1d]> <table[1d]> <table[1d]> <fct> <dbl>
1 131 529 650 621.3707273 745 869 0 2000
2 161 488 621 591.7821183 723 851 126 2040
3 159 423 598 561.0055187 711 838 126 2060
4 178 490 630 591.4048857 727 832 126 2080
5 190 528 652 607.6964160 723 829 126 2100
6 186 504 633 604.1238252 743 843 245 2040
7 151 339 535 499.0796473 662 807 245 2060
8 146 297 541 499.5963739 701 797 245 2080
9 132 233 430 432.4860327 623 764 245 2100
10 143 415 562 546.4167326 684 839 370 2040
11 151 361 561 521.7052767 686 805 370 2060
12 132 202 339 397.2122107 602 778 370 2080
13 102 128 170 228.5666202 338 562 370 2100
14 179 498 622 592.6720370 713 849 585 2040
15 141 277 494 464.1393137 650 781 585 2060
16 112 136 188 249.8091408 384 554 585 2080
17 82 97 111 132.5967960 169 273 585 2100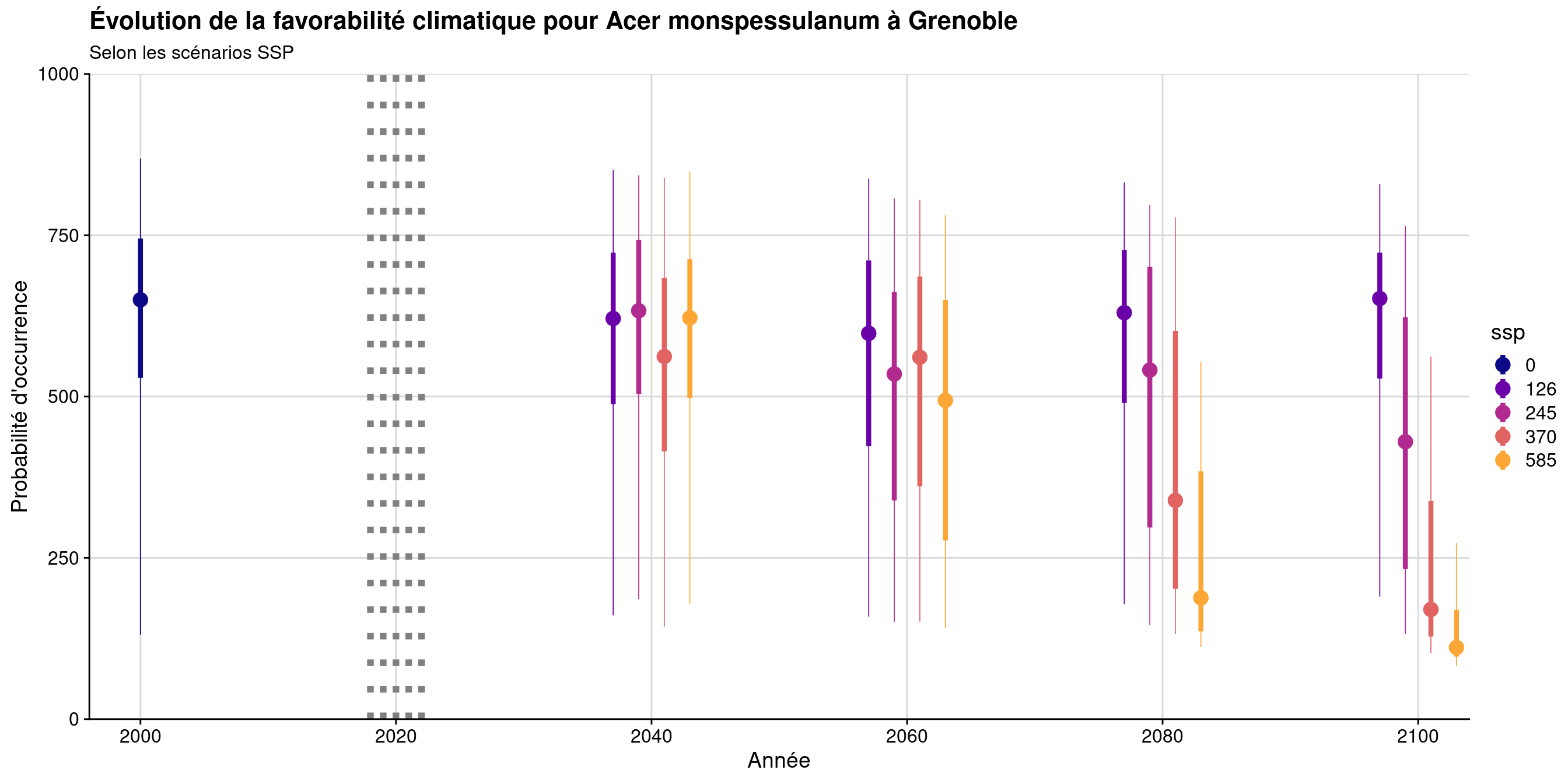
Figure 3.30: Évolution de la favorabilité climatique au cours du XXIème siècle. Le point représente la médiane sur l’étendue de la métropole (i.e. tous les pixels de la carte) ; le trait gras représente 50 % des données intermédiaires (espace inter-quartile) ; le trait fin représente le reste des données du minimum au maximum.